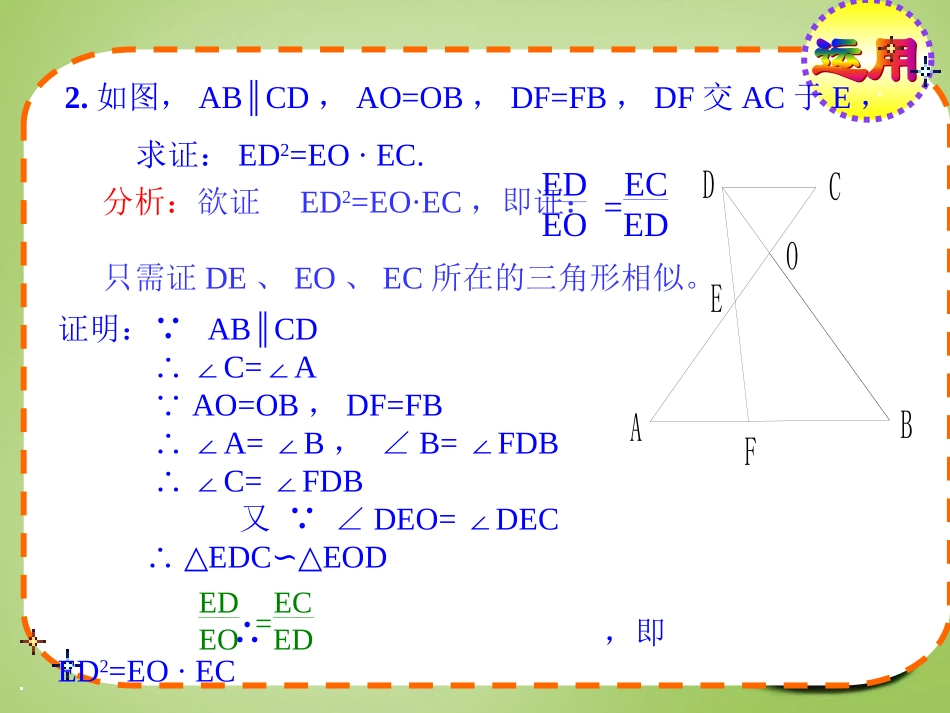
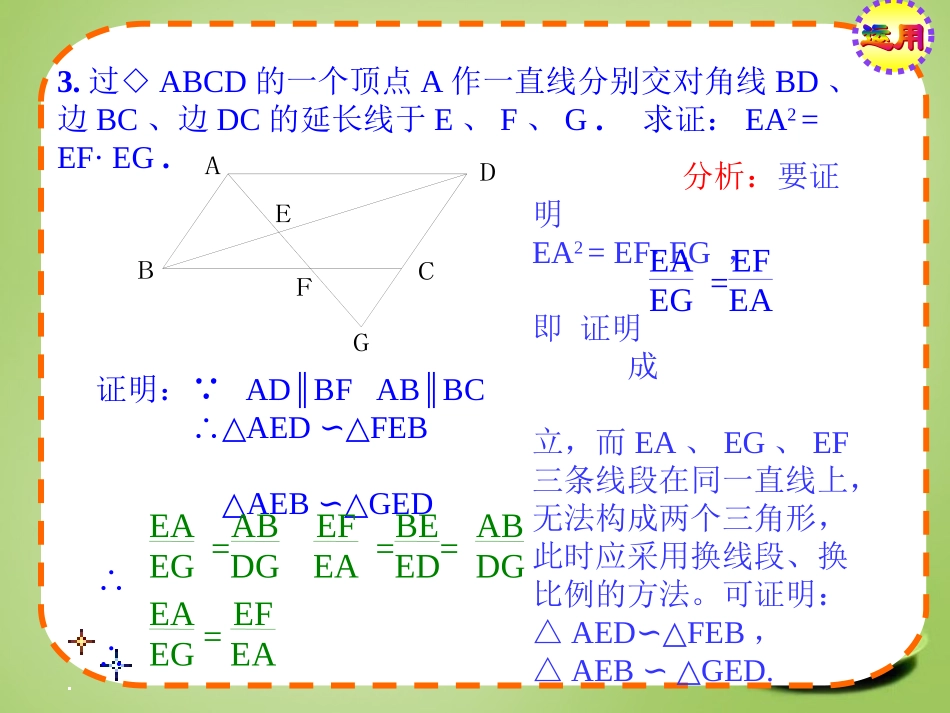
一、相似三角形的性质①相似三角形的对应角相等,对应边成比例.②相似三角形对应中线的比,对应角平分线的比,对应高的比,对应周长的比都等于相似比.③相似三角形面积的比等于相似比的平方.二.相似三角形的判定方法定理1两角对应相等的两个三角形相似.推论1平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;定理2三边对应成比例的两个三角形相似.定理3两边对应成比例,且夹角相等的两个三角形相似;定理4斜边直角边对应成比例的两个直角三角形相似.2.如图,ABCD∥,AO=OB,DF=FB,DF交AC于E,求证:ED2=EO·EC.ABCDEFO分析:欲证ED2=EO·EC,即证:只需证DE、EO、EC所在的三角形相似。EDEO=ECED证明:∵ABCD∥∴∠C=A∠∵AO=OB,DF=FB∴∠A=B∠,∠B=FDB∠∴∠C=FDB∠又∵∠DEO=DEC∠∴△EDCEOD∽△∴,即ED2=EO·ECEDEO=ECED3.过◇ABCD的一个顶点A作一直线分别交对角线BD、边BC、边DC的延长线于E、F、G.求证:EA2=EF·EG.ABCDEFG分析:要证明EA2=EF·EG,即证明成立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AEDFEB∽△,△AEBGED.∽△证明:∵ADBFABBC∥∥∴△AEDFEB∽△△AEBGED∽△∴∴EAEG=ABDGEFEA=BEED=ABDGEAEG=EFEAEAEG=EFEA4.已知在△ABC中,∠BAC=90°,ADBC⊥,E是AC的中点,ED交AB的延长线于F.求证:AB:AC=DF:AF.ADEFBC分析:因△ABCABD∽△,所以要证即证,需证△BDFDAF.∽△AFDFACABADBDACABAFDFADBD证明:∵∠BAC=90°ADBC⊥∴∠ABC+C=90°∠∠ABC+BAD=90°∠∴∠BAD=C∠∵∠ADC=90°E是AC的中点,∴ED=EC∴∠EDC=C∠∵∠EDC=BDF∠AFDFADBD∴∠BDF=C=BAD∠∠又∵∠F=F∠∴△BDFDAF.∽△∴∵∠BAC=90°,ADBC⊥∴△ABCABD∽△∴∴ADBDACABAFDFACAB5.D为△ABC的底边BC的延长线上一点,直线DF交AC于E,且∠FEA=AFE.∠求证:BD·CE=CD·BFFEDCBA由BD·CE=CD·BF,得分析:但△DBF与△DCE不相似因此,需作辅助线构造相似三角形BDBFCECD=5.D为△ABC的底边BC的延长线上一点,直线DF交AC于E,且∠FEA=AFE.∠求证:BD·CE=CD·BFFEDCBAG方法一:过点C作CGAB,∥交DF于G则△DCGDBF∽△故再证CG=CE即可CDCGBFBD=FEDCBAG方法二:过点C作CGDF,∥交AB于G故再证FG=CE即可5.D为△ABC的底边BC的延长线上一点,直线DF交AC于E,且∠FEA=AFE.∠求证BD·CE=CD·BFBDBFFGCD=FEDCBAG5.D为△ABC的底边BC的延长线上一点,直线DF交AC于E,且∠FEA=AF.∠求证:BD·CE=CD·BF方法三:过点B作BGDF,∥交DF的延长线于G故再证BG=BF即可则△DCEDBG∽△DCCEBGDB=6.如图:已知△ABC中,AD平分∠BAC,EF是AD的中垂线,EF交BC的延长线于F.求证:FD2=FC·FBFEDCBA分析:由FD2=FC·FB,得FDFBFDFC=但FD、FC、FB都在同一直线上,无法利用相似三角形.由于FD=FA,替换后可形成相似三角形.FDFBFDFC=FAFBFAFC=只要证△FABFCA∽△即可.7.已知,AB∥CDEF∥,(1)图中有几对相似的三角形?(2)线段AB、CD与EF有怎样的等量关系?FABCDE⊿EDCEBA∽⊿⊿ADCAFE∽⊿⊿BDAEDF∽⊿CDEFABAEACAECEEFCDABCDAEACEFCDAECEABCD1111证比例式(或乘积式)的常用方法证明乘积式时,可先将乘积式改为比例式(1)找相似三角形(或平行线)(2)没有相似三角形(或平行线),利用等比例转化,或利用等线段转化,或等积转化,或构造辅助线转化