高一数学三角函数苏教版知识精讲VIP免费

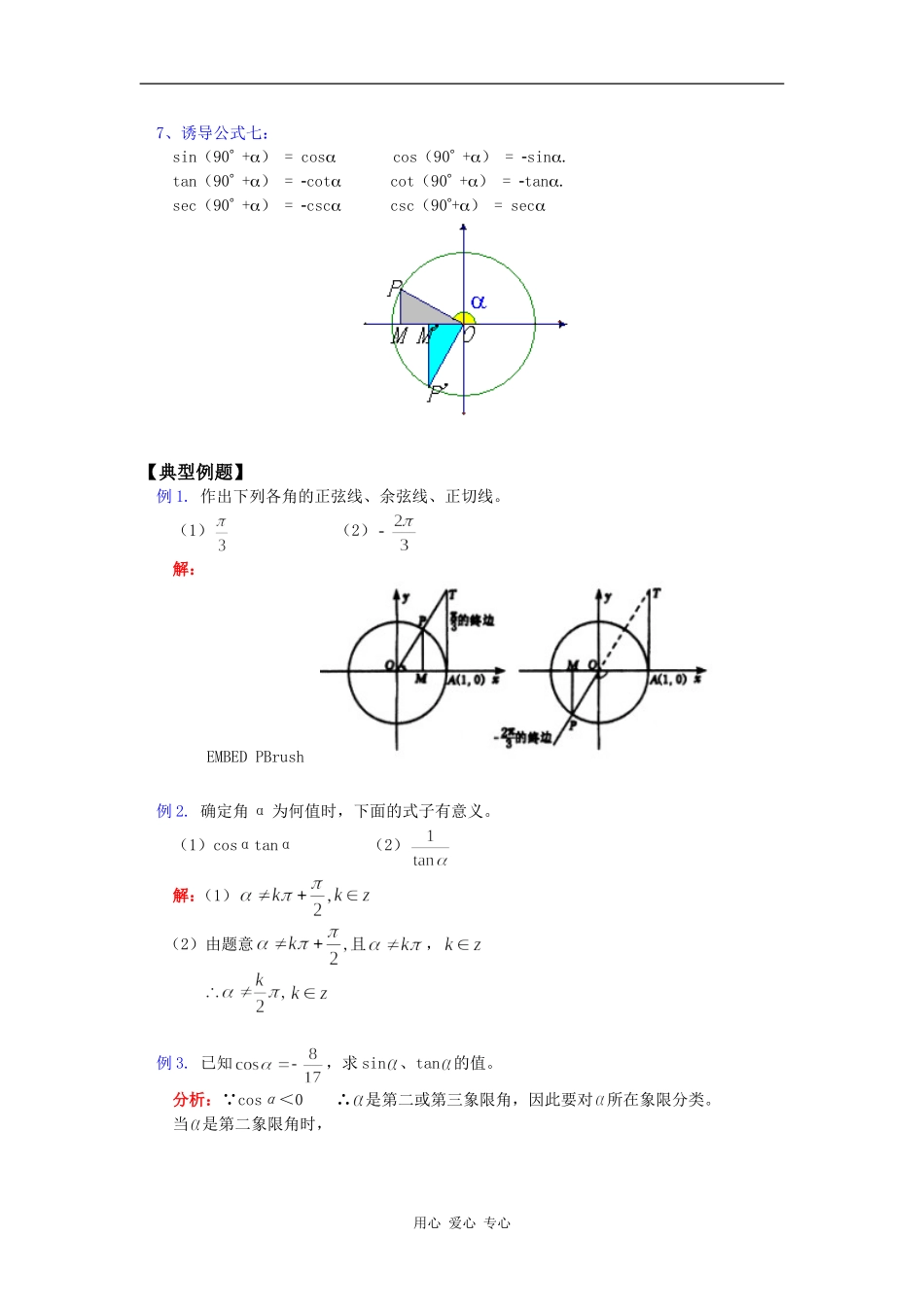
高一数学三角函数苏教版【本讲教育信息】一.教学内容：三角函数1、掌握任意角的正弦、余弦、正切的定义，会用角α的正弦线、余弦线、正切线分别表示任意角α的正弦、余弦、正切的函数值。2、掌握同角三角函数基本关系式，并会运用它们进行简单的三角函数式的化简、求值及恒等式证明。3、能借助于单位圆，推导出正弦、余弦的诱导公式，能正确运用诱导公式将任意角的三角函数化为锐角的三角函数，并解决有关三角函数求值、化简和恒等证明问题。（一）三角函数的几何表示1、有向线段：规定了方向（即规定了起点与终点）的线段称为有向线段。有向直线：规定了正方向的直线称为有向直线。有向线段的数量：有向线段AB与有向直线l的方向相同或相反，分别把它的长度加上正号与负号，这样所得的数叫做有向线段的数量。记为AB如图：AB＝3，BC＝2，CB＝－22、三角函数线的定义：有向线段MP、OM、AT都称为三角函数线（二）同角三角函数的关系1.公式：2.采用定义证明：用心爱心专心（三）诱导公式1、诱导公式一：（其中）用弧度制可写成（其中）诱导公式（一）的作用：把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切，其方法是先在0º―360º内找出与角终边相同的角，再把它写成诱导公式（一）的形式，然后得出结果。2、诱导公式二：用弧度制可表示如下：3、诱导公式三：4、诱导公式四：用弧度制可表示如下：5、诱导公式五：6、诱导公式六：sin（90）=coscos（90）=sin.tan（90）=cotcot（90）=tan.sec（90）=csccsc（90）=sec用心爱心专心7、诱导公式七：sin（90+）=coscos（90+）=sin.tan（90+）=cotcot（90+）=tan.sec（90+）=csccsc（90+）=sec【典型例题】例1.作出下列各角的正弦线、余弦线、正切线。（1）（2）解：EMBEDPBrush例2.确定角α为何值时，下面的式子有意义。（1）cosαtanα（2）解：（1）（2）由题意且，例3.已知，求sin、tan的值。分析：∵cosα＜0∴是第二或第三象限角，因此要对所在象限分类。当是第二象限角时，用心爱心专心当是第三象限时例4.已知tan，求下列各式的值。分析：思路1，可以由tan=3求出sin、cos的值，代入求解即可；思路2，可以将要求值的表达式利用同角三角函数关系，变形为含tan的表达式．解：（1）原式分子分母同除以得，原式=（2）原式的分子分母同除以得：原式=（3）用“1”的代换原式=（4）原式=例5.求下列各式的值：（1）sin（－）；（2）cos（－60º）－sin（－210º）分析：本题是诱导公式二、三的巩固性练习题。求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦，然后再用诱导公式二把它们化为锐角的正弦、余弦来求。解：（1）sin（－）=－sin（）=sin=（2）原式=cos60º+sin（180º+30º）=cos60º－sin30º=－=0用心爱心专心例6.化简：解：原式===1【模拟试题】一、选择题1.已知sinα＋cosα＝，且0＜α＜π，则tanα的值为（）A.B.C.D.2.若sin4θ＋cos4θ＝1，则sinθ＋cosθ的值为（）A.0B.1C.－1D.±13.化简sin（－2）+cos（－2－π）·tan（2－4π）所得的结果是（）A.2sin2B.0C.－2sin2D.－1二、填空题4.已知，则的值等于。5.=。6.化简：所得的结果是。三、解答题7.已知，求的值。8.求下列三角函数值：（1）；（2）；（3）；（4）9.化简：10.求值：11.已知，，则的值是_____。12.设f（θ）=，求f（）的值。补充题的答案与提示：=用心爱心专心试题答案一、选择题1.A2.D3.C二、填空题4.±5.06.－2cosα三、解答题7.∵，∴在Ⅰ、Ⅳ象限，当α在Ⅰ象限时，∴当在Ⅳ象限时∴8.（1）－（2）－（3）（4）9.提示：原式==110.－提示：原式==－11.提示：已知条件即，故12.提示：==用心爱心专心