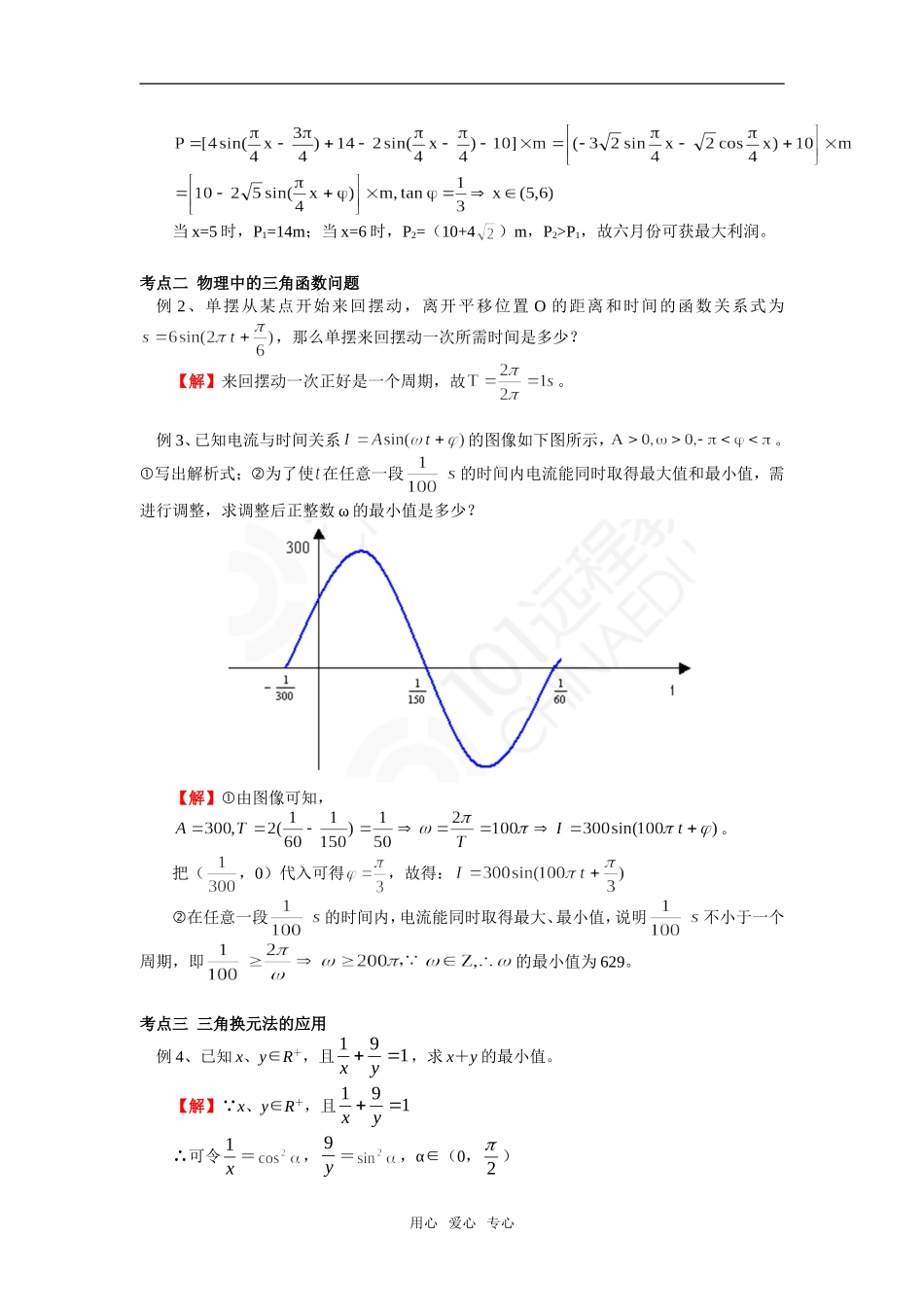
高一数学三角函数的简单应用北师大版【本讲教育信息】一、教学内容:三角函数的简单应用圆周运动、简谐振动中的三角函数模型;三角恒等变换与三角函数的性质;三角形中的三角函数问题;二、学习目标1、了解单摆运动、波的传播、交流电等物理现象中的三角函数模型,学会运用三角函数来分析和理解;2、会选择合适的三角恒等变换对三角函数式进行恒等变形,从而研究其函数性质(值域、周期、对称性、单调性等);3、会处理生活中简单的三角问题;4、通过三角恒等变换的应用,提高推理能力和运算能力。三、知识要点1、简谐振动中的三角函数——其中,A称为振幅,称为初相,称为相位;称为周期,称为频率。2、三角恒等变换的常用技巧——切弦互化、公式逆用、“1”的拆变、整体处理角、统一角度、统一函数类型与幂次等等;3、测量中的简单的三角问题——张角(视角)、俯角、仰角;方位角;坡度、跨度;经度、纬度四、考点解析与典型例题考点一生活中的三角建模问题例1、某商品一年内出厂价格在10元的基础上按月份随正弦曲线波动,已知3月份达到最高价格12元,7月份价格最低为8元,该商品在商店内的销售价格在14元基础上按月份随正弦曲线波动,5月份销售价格最高为18元,9月份销售价格最低为10元,假设商店每月购进这种商品m件,且当月售完,你估计哪个月份盈利最大?【分析】由题意可知,该问题中存在着正弦函数关系,可通过设变量,找出变量间的正弦函数关系进行求解。【解】设月份为x,则由题意可知:出厂价格函数为可解得:,所以,出厂价格函数为:;设销售价格函数为可解得,从而销售价格函数为:。当进货数量为m件时,利润=进货数量×(销售价格-出厂价格),从而利润为用心爱心专心当x=5时,P1=14m;当x=6时,P2=(10+4)m,P2>P1,故六月份可获最大利润。考点二物理中的三角函数问题例2、单摆从某点开始来回摆动,离开平移位置O的距离和时间的函数关系式为,那么单摆来回摆动一次所需时间是多少?【解】来回摆动一次正好是一个周期,故。例3、已知电流与时间关系的图像如下图所示,。写出解析式;为了使在任意一段的时间内电流能同时取得最大值和最小值,需进行调整,求调整后正整数ω的最小值是多少?【解】由图像可知,。把(,0)代入可得,故得:在任意一段的时间内,电流能同时取得最大、最小值,说明不小于一个周期,即的最小值为629。考点三三角换元法的应用例4、已知x、y∈R+,且191yx,求x+y的最小值。【解】 x、y∈R+,且191yx∴可令x1=,y9=,α∈(0,2)用心爱心专心∴x+y==10+(+)≥10+6=16当且仅当=即=3时等号成立【说明】三角换元法是一种应用十分广泛的方法,对有关平方和的等式(或方程)、有关平方差的等式或方程和有关正数的和差的式子等均可考虑三角换元。考点四三角形中的三角函数问题例5、在Rt△ABC内有一内接正方形,它的一条边在斜边BC上.(1)设AB=a,∠ABC=θ,求△ABC的面积P与正方形面积Q。(2)当θ变化时求P/Q的最小值.解:(1)(2)由(1)【总结】步骤:设自变量,建立三角函数关系式,求函数的最值(注意角的范围)考点五立体几何中的三角函数问题例6、求半径为1的球的外切圆锥的全面积的最小值新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆【解】利用轴截面,设球心与底角的连线与底边的夹角为a,则。考点六测量中的三角函数例7、如图,塔AB和楼CD的水平距离为80米,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高与楼高(精确到0.01米)。(参考数据:2=1.41421…,3=1.73205…)用心爱心专心【分析】此题可先通过解Rt△ABD求出塔高AB,再利用CE=BD=80米,解Rt△AEC,求出AE,最后求出CD=BE=AB-AE。【解】在Rt△ABD中,BD=80米,∠BDA=60°∴AB=BD·tan60°56.13838060tan0BD(米)在Rt△AEC中,EC=BD=80米,∠ACE=45°∴AE=CE=80米∴CD=BE=AB-AE=56.5880380(米)答:塔AB的高约为138.56米,楼CD的高约为58.56米。五、数学思想方法三角函数是中...