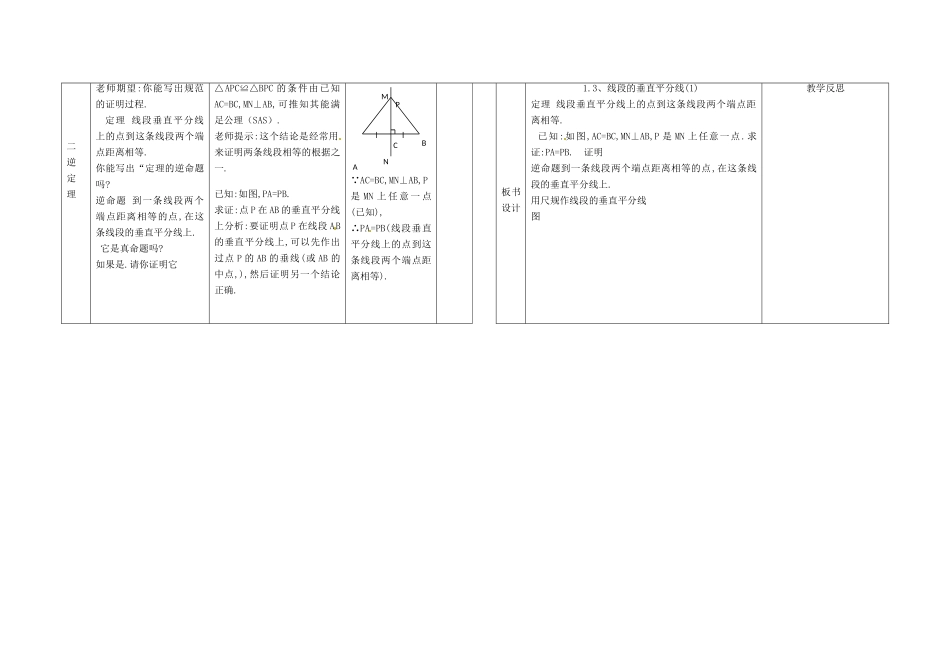
课题1.3、线段的垂直平分线(1)教学环节教学内容教学方法(师生活动)教学预期及调整时间分配教学目标1.要求学生掌握线段垂直平分线的性质定理及判定定理,能够利用这两个定理解决一些问题。2.能够证明线段垂直平分线的性质定理及判定定理。3.通过探索、猜测、证明的过程,进一步拓展学生的推理证明意识和能力。三尺规作图四巩固练习∵PA=PB(已知),∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.用尺规作线段的垂直平分线已知:线段AB,如图.求作:线段AB的垂直平分作法:1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.2.作直线CD则直线CD就是线段AB的垂直平分线教学重点线段垂直平分线性质定理及其逆定理。教学难点线段垂直平分线的性质定理及其逆定理的内涵和证明。教学关键线段垂直平分线性质定理及其逆定理的掌握。教学方法观察实践法,分组讨论法,讲练结合法,自主探究法教学环节教学内容教学方法(师生活动)教学预期及调整时间分配一性质定理我们曾经利用折纸的方法得到:线段垂直平分线上的点到这条线段两个端点距离相等.你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,就需要证明PA,PB所在的△APC≌△BPC,而ACBPMNEDABC二逆定理老师期望:你能写出规范的证明过程.定理线段垂直平分线上的点到这条线段两个端点距离相等.你能写出“定理的逆命题吗?逆命题到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它△APC≌△BPC的条件由已知AC=BC,MN⊥AB,可推知其能满足公理(SAS).老师提示:这个结论是经常用来证明两条线段相等的根据之一.已知:如图,PA=PB.求证:点P在AB的垂直平分线上分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中点,),然后证明另一个结论正确.∵AC=BC,MN⊥AB,P是MN上任意一点(已知),∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).板书设计1.3、线段的垂直平分线(1)定理线段垂直平分线上的点到这条线段两个端点距离相等.已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.证明逆命题到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.用尺规作线段的垂直平分线图教学反思ACBPMN