北京市清华附中212届高三数学考前适应性训练试题 文VIP免费

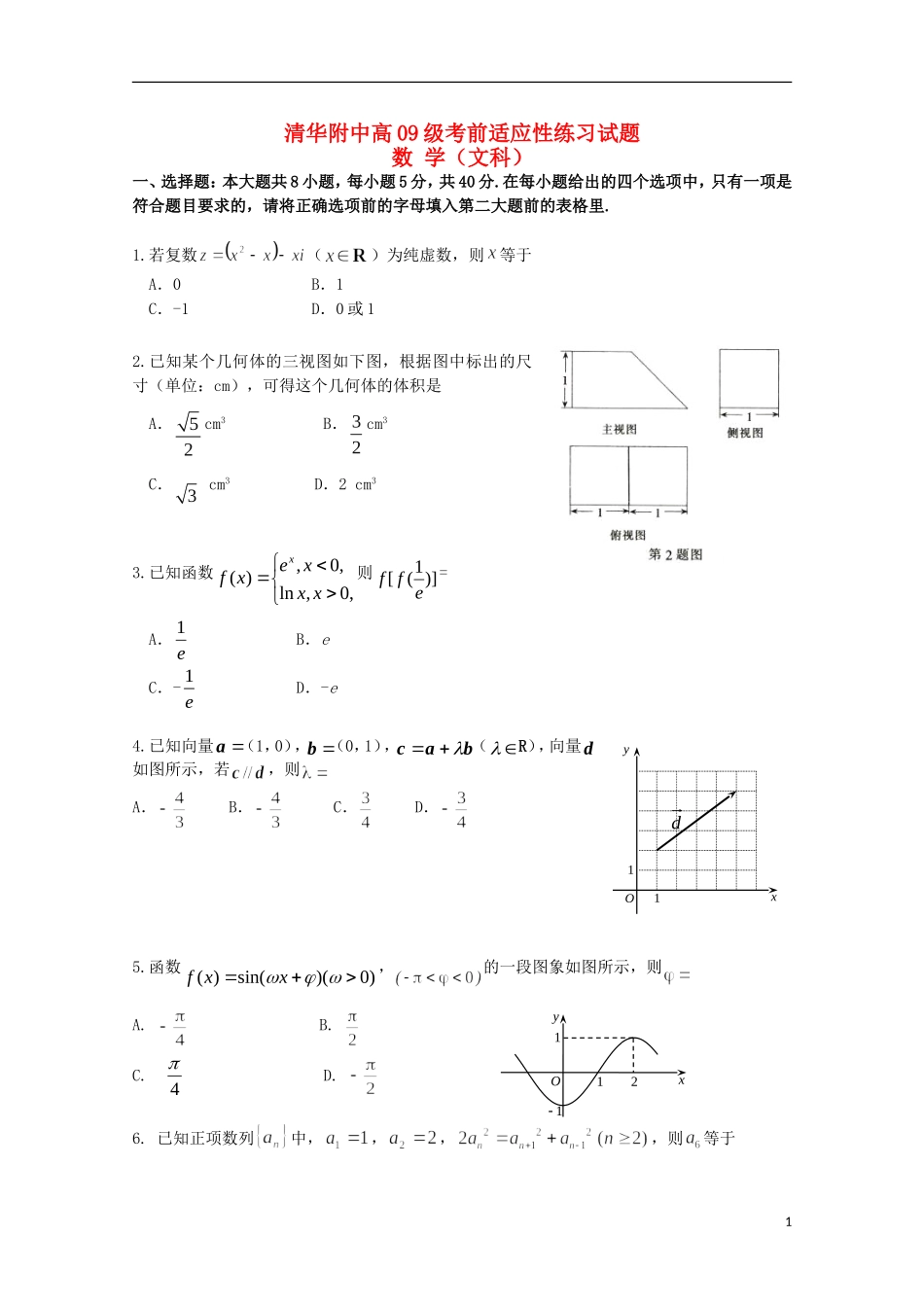
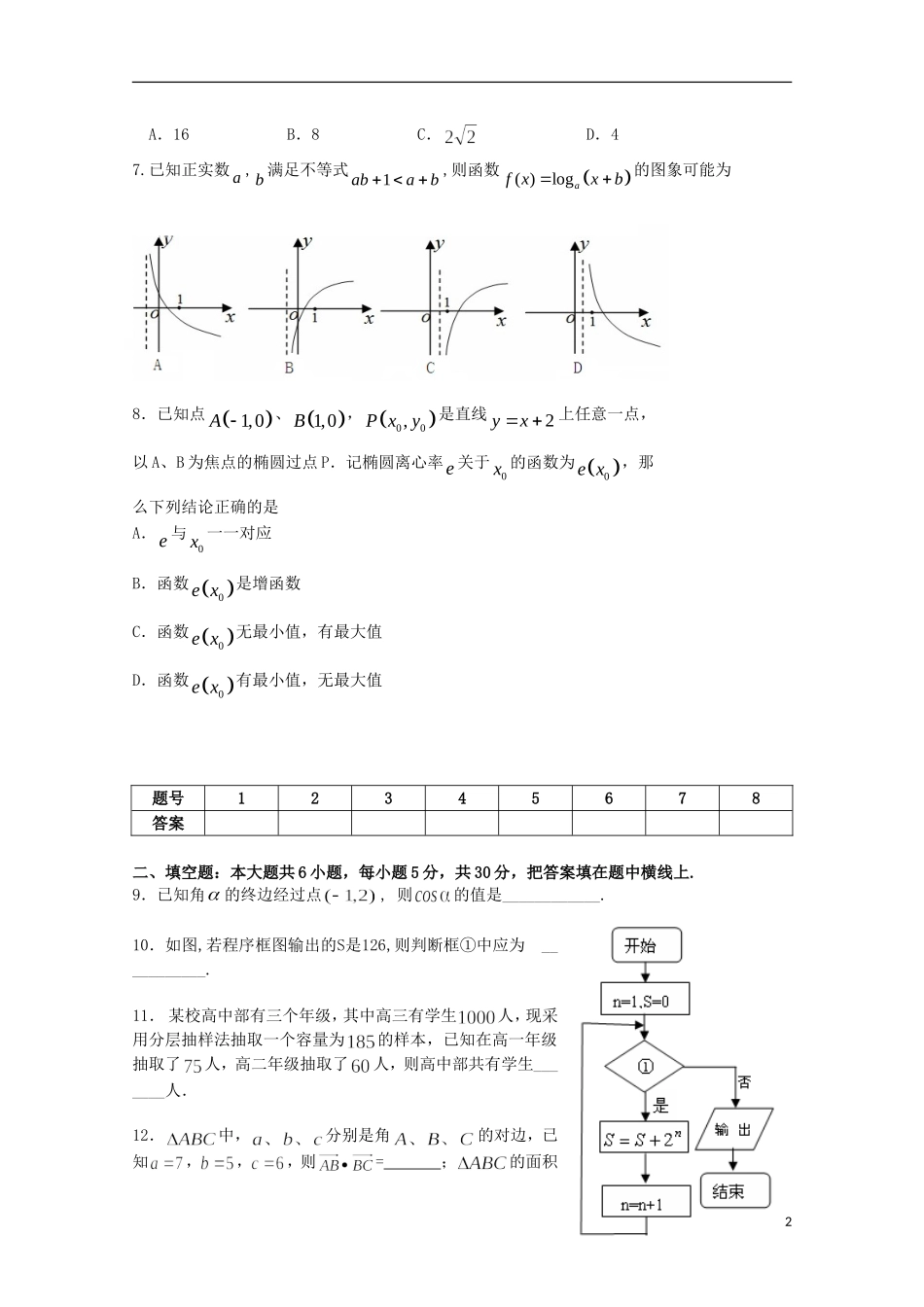
清华附中高09级考前适应性练习试题数学（文科）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母填入第二大题前的表格里.1.若复数（）为纯虚数，则等于A．0B．1C．-1D．0或12.已知某个几何体的三视图如下图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是A．52cm3B．32cm3C．3cm3D．2cm33.已知函数,0,ln,0,)(xxxexfx则)]1([eff=A．e1B．eC．-e1D．-e4.已知向量a（1，0），b（0，1），bac（R），向量d如图所示，若，则A．B．C．D．5.函数()sin()(0)fxx，的一段图象如图所示，则A.B.C.4D.6.已知正项数列中，，，，则等于1dOyx11xyO1211A．16B．8C．D．47.已知正实数a,b满足不等式1abab,则函数()logafxxb的图象可能为8．已知点1,0A、1,0B，00,Pxy是直线2yx上任意一点，以A、B为焦点的椭圆过点P．记椭圆离心率e关于0x的函数为0ex，那么下列结论正确的是A．e与0x一一对应B．函数0ex是增函数C．函数0ex无最小值，有最大值D．函数0ex有最小值，无最大值题号12345678答案二、填空题：本大题共6小题，每小题5分，共30分，把答案填在题中横线上.9．已知角的终边经过点,则的值是____________.10．如图,若程序框图输出的S是126,则判断框①中应为___________.11．某校高中部有三个年级，其中高三有学生人，现采用分层抽样法抽取一个容量为的样本，已知在高一年级抽取了人，高二年级抽取了人，则高中部共有学生_______人．12．中，分别是角的对边，已知，，，则=；的面积2BADCFE（第16题）为．13．已知不等式组表示的平面区域的面积为，点，则的最大值为.14．曲线是平面内到定点的距离与到定直线的距离之和为3的动点的轨迹.则曲线与轴交点的坐标是；又已知点（为常数），那么的最小值=.三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.15．(本小题满分13分)已知函数，（Ⅰ）求函数的最小正周期；（Ⅱ）记的内角A,B,C的对边长分别为，若，求的值。16.(本小题满分14分)如图，在四棱锥中，底面为矩形，平面平面，，，为的中点，求证：（Ⅰ）平面；（Ⅱ）平面平面；（Ⅲ）求四棱锥的体积.17.(本小题满分13分)从含有两件正品和一件次品的3件产品中，每次任取1件（Ⅰ）每次取出后不放回，连续取两次，求取出的产品中恰有一件次品的概率；（Ⅱ）每次取出后放回，连续取两次，求取出的产品中恰有一件次品的概率；318.(本小题满分13分)已知函数,其中为常数,且.（I）若曲线在点（1，）处的切线与直线垂直，求的值；（II）若函数在区间[1，2]上的最小值的表达式.19.（本小题满分14分）已知椭圆C：)0(12222babyax的上顶点为，两个焦点为、，为正三角形且周长为6.（Ⅰ）求椭圆C的标准方程；（Ⅱ）已知圆O:222Ryx，若直线l与椭圆C只有一个公共点M，且直线l与圆O相切于点N；求||MN的最大值．20.（本小题共13分）将这个数随机排成一列，得到的一列数称为的一个排列.定义为排列的波动强度.（Ⅰ）当时，写出排列的所有可能情况及所对应的波动强度；（Ⅱ）当时，求的最大值，并指出所对应的一个排列.4文科考前适应性练习参考答案：选择：1、B2、B3、A4、C5、D6、D7、B8、C填空：9、10、?6n11、370012、，13、614、解答：15解（Ⅰ）所以函数的最小正周期为。（Ⅱ）由得,即又因为,所以所以,即.因为所以由正弦定理,得故当当故的值为1或2.17、（1）（2）18解：()5（I）因为曲线在点（1，）处的切线与直线垂直，所以，即(II)当时，在（1，2）上恒成立，这时在[1，2]上为增函数当时，由得，对于有在[1，a]上为减函数，对于有在[a，2]上为增函数，当时，在（1，2）上恒成立，这时在[1，2]上为减函数，.19、解：（Ⅰ）解：由题设得解得：3,2ba，故C的方程为13422yx.（Ⅱ）直线l的斜率显然存在，设直线l的方程为tkxy，由直线l与圆O相切，得2222)1(,1||rktktr①由01248)43(13422222tktxxktkxyyx，因为直线l与椭圆C相切，所以0)124)(43(4)8(222...