二倍角的正弦、余弦、正切知识精讲 苏教版VIP免费

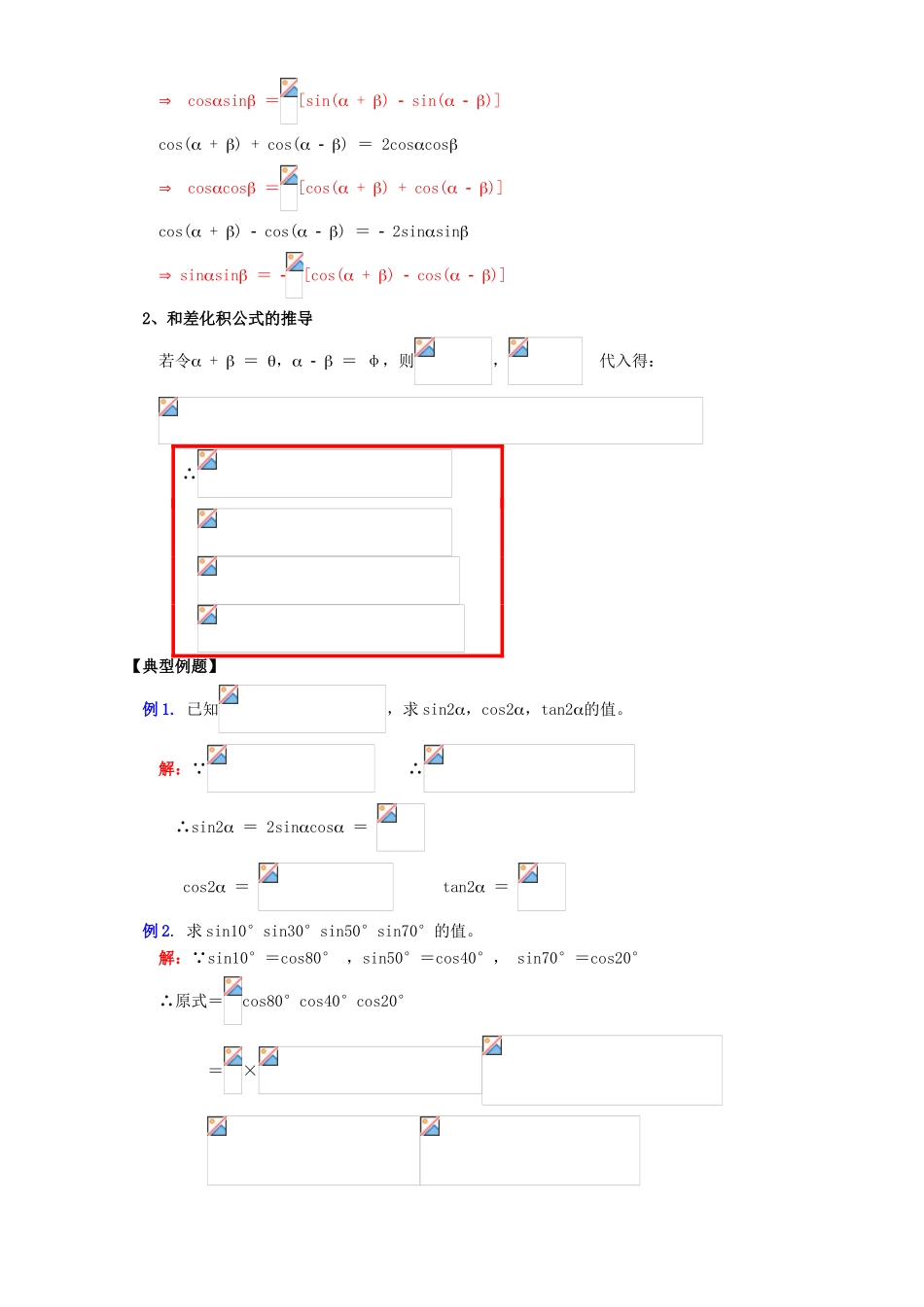
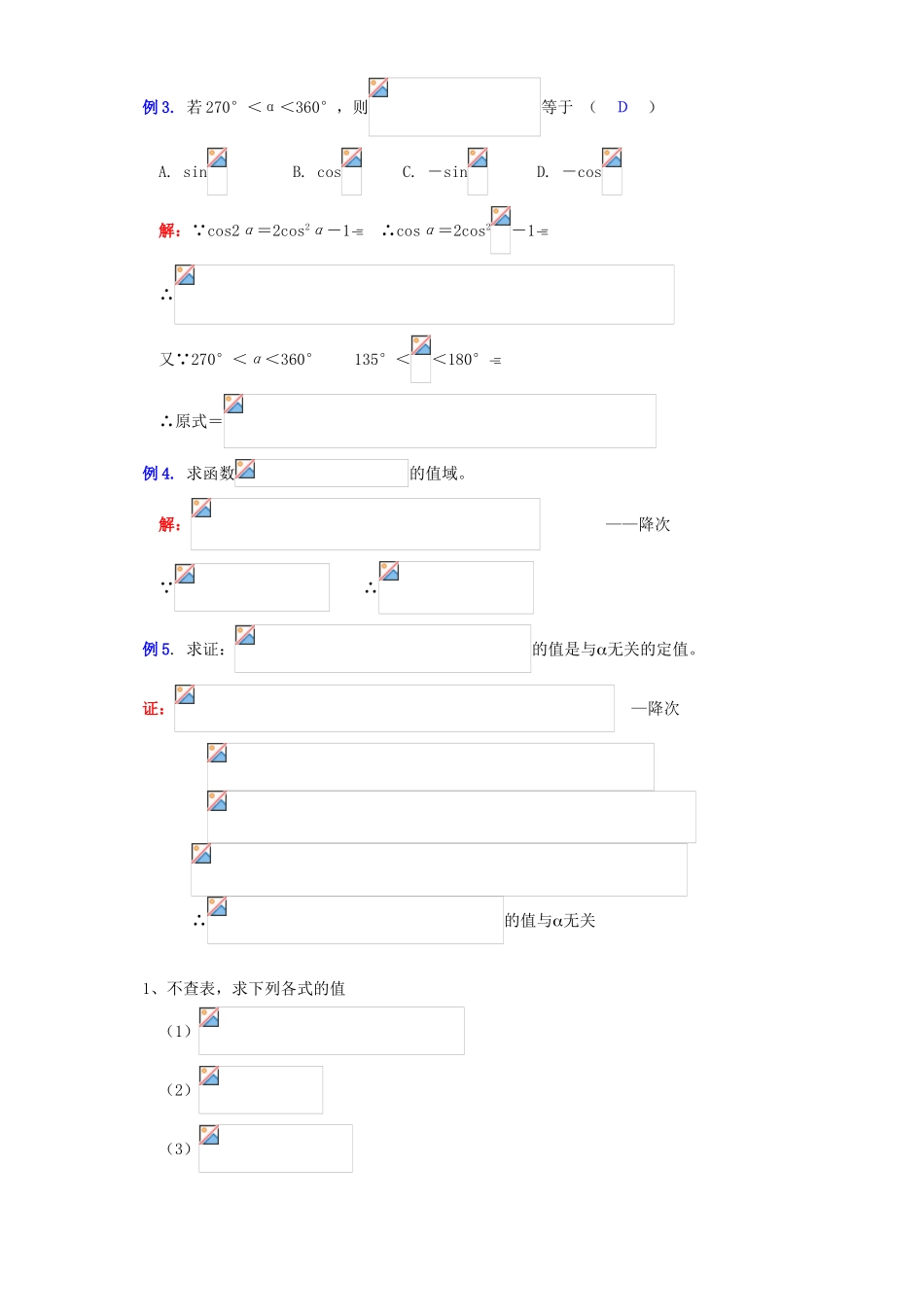
二倍角的正弦、余弦、正切知识精讲一.本周教学内容：二倍角的正弦、余弦、正切二、本周教学目标：1、掌握二倍角的正弦、余弦、正切公式；2、能用上述公式进行简单的求值、化简、恒等证明；3、通过和差化积公式和积化和差公式的推导，提高三角变换的能力。三、本周知识要点：（一）二倍角公式的推导在公式，，中，当时，得到相应的一组公式：；；；因为，所以公式可以变形为或公式，，，统称为二倍角的三角函数公式，简称为二倍角公式。（二）二倍角公式注意：（1）二倍角公式的作用在于用单角的三角函数来表达二倍角的三角函数，它适用于二倍角与单角的三角函数之间的互化问题。（2）二倍角公式为仅限于是的二倍的形式，尤其是“倍角”的意义是相对的。（3）二倍角公式是从两角和的三角函数公式中，取两角相等时推导出，记忆时可联想相应角的公式。（4）熟悉“倍角”与“二次”的关系（升角—降次，降角—升次）（5）特别注意公式的三角表达形式，且要善于变形：这两个形式今后常用。（三）几个三角恒等式1、积化和差公式的推导sin(+)+sin()＝2sincossincos＝[sin(+)+sin()]sin(+)sin()＝2cossincossin＝[sin(+)sin()]cos(+)+cos()＝2coscoscoscos＝[cos(+)+cos()]cos(+)cos()＝2sinsinsinsin＝[cos(+)cos()]2、和差化积公式的推导若令+＝，＝φ，则，代入得：∴【典型例题】例1.已知，求sin2，cos2，tan2的值。解：∵∴∴sin2＝2sincos＝cos2＝tan2＝例2.求sin10°sin30°sin50°sin70°的值。解：∵sin10°＝cos80°，sin50°＝cos40°，sin70°＝cos20°∴原式＝cos80°cos40°cos20°＝×例3.若270°＜α＜360°，则等于（Ｄ）A.sinB.cosC.－sinD.－cos解：∵cos2α＝2cos2α－1∴cosα＝2cos2－1∴又∵270°＜α＜360°135°＜＜180°∴原式＝例4.求函数的值域。解：——降次∵∴例5.求证：的值是与无关的定值。证：—降次∴的值与无关1、不查表，求下列各式的值（1）（2）（3）（4）2、求值：cos280°＋sin250°－sin190°·cos320°3、求的值。4、化简：cos20cos40cos805、求证：[sin(1+sin)+cos(1+cos)]×[sin(1sin)+cos(1cos)]＝sin26、化简下列各式：（可直接写答案）（1）（2）（3）2sin2157.51＝（4）[参考答案]1、解：（1）（2）（3）（4）2、解：原式＝＋sin10°cos40°＝1＋×2×（－sin30°sin50°）＋sin10°cos40°＝1－sin50°＋（sin50°－sin30°）＝1－＝3、解：原式＝4、解：原式＝5、证：左边＝(sin+sin2+cos+cos2)×(sinsin2+coscos2)＝(sin+cos+1)×(sin+cos1)＝(sin+cos)21＝2sincos＝sin2＝右边∴原式得证6、（1）（2）（3）（4）