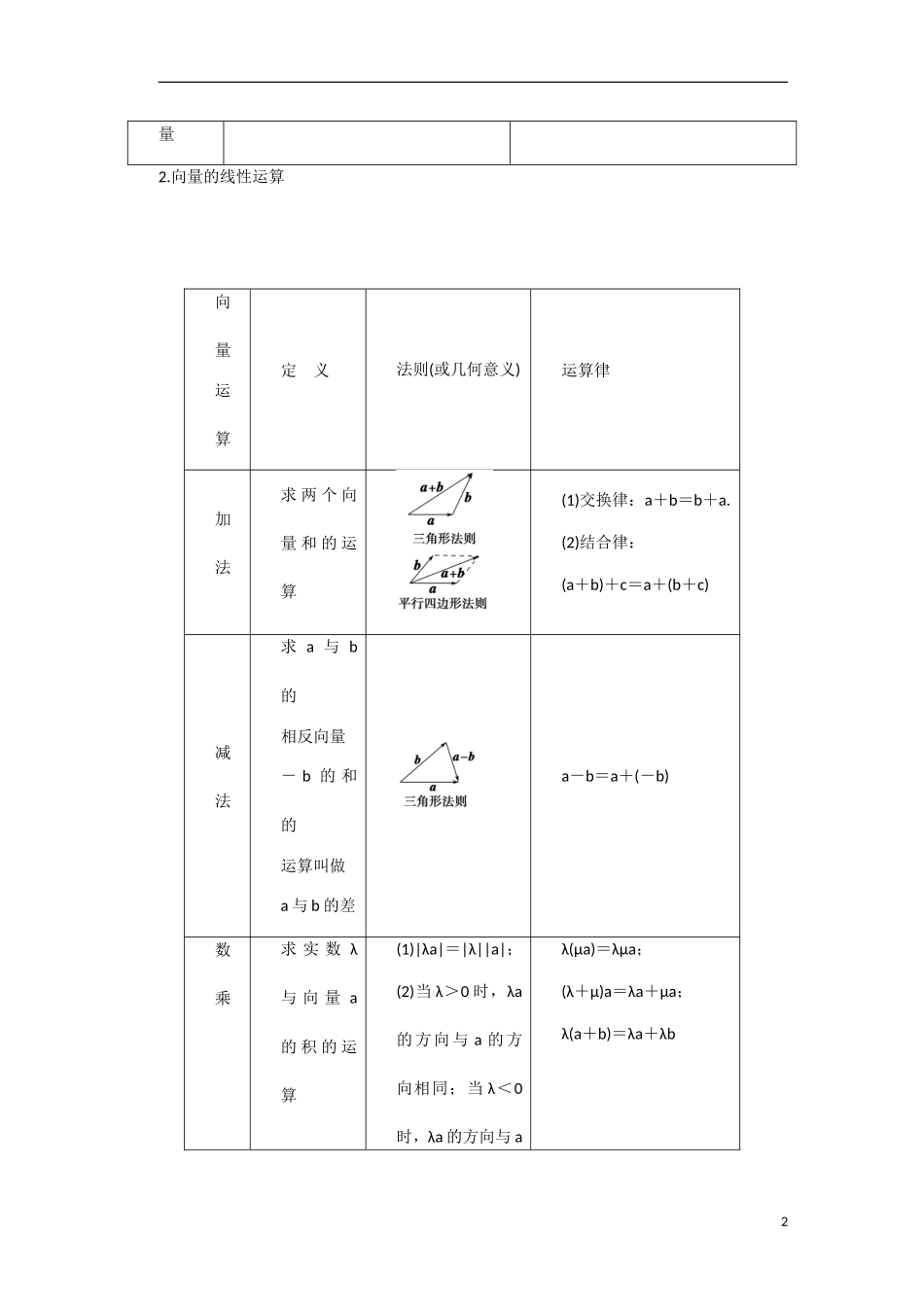
第1讲平面向量的概念及线性运算最新考纲1.了解向量的实际背景;2.理解平面向量的概念,理解两个向量相等的含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,并理解其几何意义;5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义;6.了解向量线性运算的性质及其几何意义.INCLUDEPICTURE"基础诊断.TIF"\*MERGEFORMAT知识梳理1.向量的有关概念名称定义备注向量既有大小又有方向的量;向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量长度为零的向量;其方向是任意的记作0单位向量长度等于1个单位的向量非零向量a的单位向量为±平行向量方向相同或相反的非零向量0与任一向量平行或共线共线向量方向相同或相反的非零向量又叫做共线向量相等向量长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向长度相等且方向相反的向量0的相反向量为01量2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c)减法求a与b的相反向量-b的和的运算叫做a与b的差a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与aλ(μa)=λμa;(λ+μ)a=λa+μa;λ(a+b)=λa+λb2的方向相反;当λ=0时,λa=03.共线向量定理向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得b=λa.诊断自测1.判断正误(在括号内打“√”或“×”)INCLUDEPICTURE"手.tif"\*MERGEFORMAT精彩PPT展示(1)若向量a,b共线,则向量a,b的方向相同.(×)(2)若a∥b,b∥c,则a∥c.(×)(3)向量AB与向量CD是共线向量,则A,B,C,D四点在一条直线上.(×)(4)若a∥b,则∃λ∈R使b=λa.(×)2.(2015·东北三省四市联考)在四边形ABCD中,若AC=AB+AD,则四边形ABCD一定是()A.矩形B.菱形C.正方形D.平行四边形解析依题意得AB+BC=AB+AD,BC=AD,因此BC∥AD,且BC=AD,四边形ABCD是平行四边形,故选D.答案D3.(2014·新课标全国Ⅰ卷)设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=()A.ADB.ADC.BCD.BC解析设AB=a,AC=b,则EB=-b+a,FC=-a+b,从而EB+FC=+=(a+b)=AD,故选A.3答案A4.设a与b是两个不共线向量,且向量a+λb与2a-b共线,则λ=________.解析由题意知,a+λb=k(2a-b),则有所以k=,λ=-.答案-5.(人教A必修4P92A12改编)已知▱ABCD的对角线AC和BD相交于O,且OA=a,OB=b,则DC=______,BC=________(用a,b表示).解析如图,DC=AB=OB-OA=b-a,BC=OC-OB=-OA-OB=-a-b.答案b-a-a-bINCLUDEPICTURE"考点突破.tif"\*MERGEFORMAT考点一平面向量的有关概念【例1】给出下列命题:①若|a|=|b|,则a=b;②若A,B,C,D是不共线的四点,则AB=DC是四边形ABCD为平行四边形的充要条件;③若a=b,b=c,则a=c;④若ab∥,bc∥,则ac.∥其中正确命题的序号是()A.②③B.②④C.③④D.②③④解析①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确. AB=DC,∴|AB|=|DC|且AB∥DC,又A,B,C,D是不共线的四点,∴四边形ABCD为平行四边形;反之,若四边形ABCD为平行四边形,则|AB|=|DC|,AB∥DC且AB,DC方向相同,因此,AB=DC.4③正确. a=b,∴a,b的长度相等且方向相同,又b=c,∴b,c的长度相等且方向相同,∴a,c的长度相等且方向相同,故a=c.④不正确.当b=0时,a,c可能不平行.综上所述,正确命题的序号是②③.答案A规律方法(1)相等向量具有传递性,非零向量的平行也具有传递性.(2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.(4)非零向量a与的关系:是与a同方向的单位向量.【训练1】给出下列命题:①两个具有公共终点的向量,一定是共线向量;②两个向量不能比较大小,但它们的模能比较大小;③若λa=0(λ为实数),则λ必为零;④已知λ,μ为实数,若λa=μb,则a与b共线.其中错误命题的个数为()A.1B.2C.3D.4解析①错误.两...