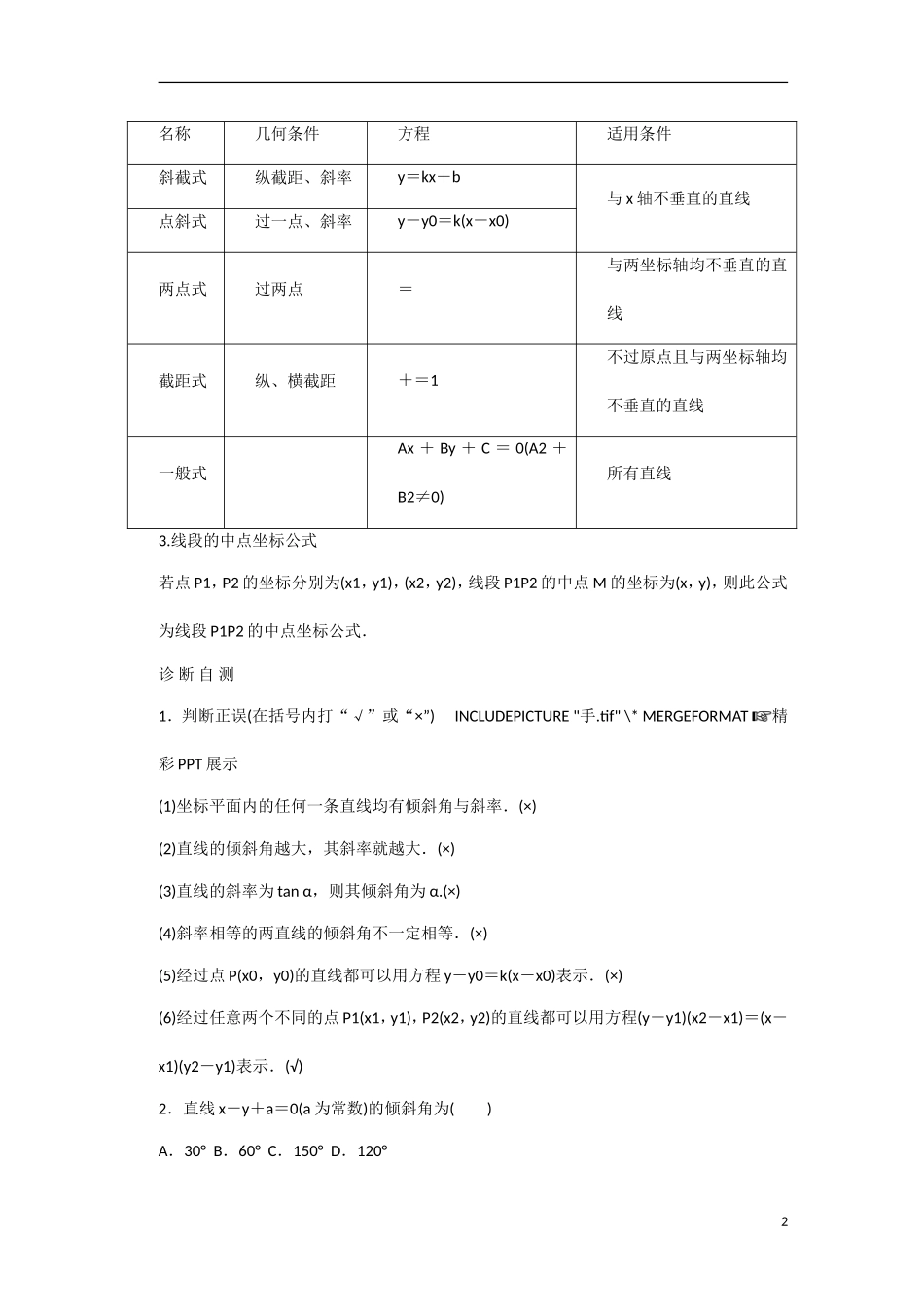
第1讲直线的方程最新考纲1.在平面直角坐标系中,结合具体图形,确定直线位置的几何要素;2.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式;3.掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.INCLUDEPICTURE"基础诊断.TIF"\*MERGEFORMAT知识梳理1.直线的倾斜角与斜率(1)直线的倾斜角①定义:当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角;②规定:当直线l与x轴平行或重合时,规定它的倾斜角为0;③范围:直线的倾斜角α的取值范围是[0,π).(2)直线的斜率①定义:当直线l的倾斜角α≠时,其倾斜角α的正切值tanα叫做这条直线的斜率,斜率通常用小写字母k表示,即k=tan__α;②斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k=.2.直线方程的五种形式1名称几何条件方程适用条件斜截式纵截距、斜率y=kx+b与x轴不垂直的直线点斜式过一点、斜率y-y0=k(x-x0)两点式过两点=与两坐标轴均不垂直的直线截距式纵、横截距+=1不过原点且与两坐标轴均不垂直的直线一般式Ax+By+C=0(A2+B2≠0)所有直线3.线段的中点坐标公式若点P1,P2的坐标分别为(x1,y1),(x2,y2),线段P1P2的中点M的坐标为(x,y),则此公式为线段P1P2的中点坐标公式.诊断自测1.判断正误(在括号内打“√”或“×”)INCLUDEPICTURE"手.tif"\*MERGEFORMAT精彩PPT展示(1)坐标平面内的任何一条直线均有倾斜角与斜率.(×)(2)直线的倾斜角越大,其斜率就越大.(×)(3)直线的斜率为tanα,则其倾斜角为α.(×)(4)斜率相等的两直线的倾斜角不一定相等.(×)(5)经过点P(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示.(×)(6)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.(√)2.直线x-y+a=0(a为常数)的倾斜角为()A.30°B.60°C.150°D.120°2解析直线的斜率为k=tanα=,又因为0°≤α<180°,所以α=60°.答案B3.如果A·C<0,且B·C<0,那么直线Ax+By+C=0不通过()A.第一象限B.第二象限C.第三象限D.第四象限解析由已知得直线Ax+By+C=0在x轴上的截距->0,在y轴上的截距->0,故直线经过一、二、四象限,不经过第三象限.答案C4.已知直线l经过点P(-2,5),且斜率为-,则直线l的方程为()A.3x+4y-14=0B.3x-4y+14=0C.4x+3y-14=0D.4x-3y+14=0解析由点斜式,得y-5=-(x+2),即3x+4y-14=0.答案A5.(人教A必修2P100A9改编)过点P(2,3)且在两轴上截距相等的直线方程为________.解析当截距为0时,直线方程为3x-2y=0;当截距不为0时,设直线方程为+=1,则+=1,解得a=5.所以直线方程为x+y-5=0.答案3x-2y=0或x+y-5=0INCLUDEPICTURE"考点突破.tif"\*MERGEFORMAT考点一直线的倾斜角与斜率【例1】(1)设直线l的方程为x+ycosθ+3=0(θR)∈,则直线l的倾斜角α的范围是()A.[0,π)B.C.D.∪(2)经过P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的倾斜角α的范围是________.3解析(1)当cosθ=0时,方程变为x+3=0,其倾斜角为;当cosθ≠0时,由直线方程可得斜率k=-. cosθ∈[-1,1]且cosθ≠0,∴k∈(-∞,-1][1∪,+∞),即tanα∈(-∞,-1][1∪,+∞),又α[0∈,π),∴α∈∪.综上知,倾斜角的范围是,故选C.(2)法一如图所示,kPA==-1,kPB==1,由图可观察出:直线l倾斜角α的范围是∪.深度思考第(2)小题同学们的解法应该多数是求kPA,kPB,再根据图象观察出倾斜角α的范围,但是还有一种方法不妨试一试,在线性规划中提到过.法二由题意知,直线l存在斜率.设直线l的斜率为k,则直线l的方程为y+1=kx,即kx-y-1=0. A,B两点在直线的两侧或其中一点在直线l上,∴(k+2-1)(2k-1-1)≤0,即2(k+1)(k-1)≤0,∴-1≤k≤1.∴直线l的倾斜角α的范围是∪.答案(1)C(2)∪规律方法(1)由直线倾斜角的取值范围求斜率的取值范围或由斜率的取值范围求直线倾4斜角的取值范围时,常借助正切函数y=t...