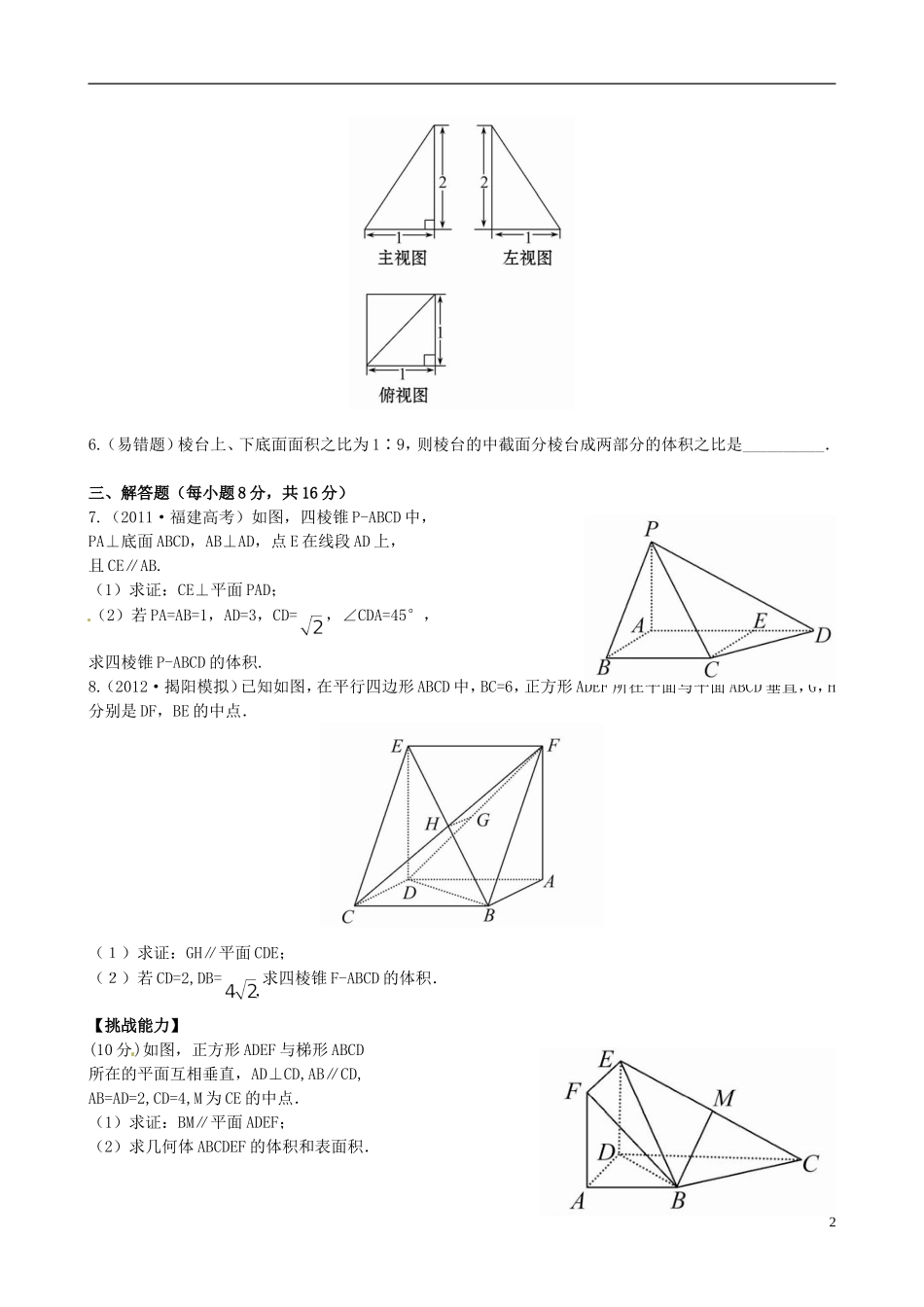
"【世纪金榜】高中数学1.7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积课时提能演练北师大版必修2"(30分钟50分)一、选择题(每小题4分,共16分)1.如图,是一个几何体的主视图、左视图、俯视图,主视图,左视图都是矩形,则该几何体的体积是()(A)24(B)12(C)8(D)42.若正方体的表面积增为原来的2倍,那么它的体积增为原来的()(A)2倍(B)4倍(C)倍(D)2倍3.(2012·浙江高考)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是()(A)1cm3(B)2cm3(C)3cm3(D)6cm34.正六棱台的两底面的边长分别为a和2a,高为a,则它的体积为()(A)(B)(C)(D)二、填空题(每小题4分,共8分)5.已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的体积为_______.16.(易错题)棱台上、下底面面积之比为1∶9,则棱台的中截面分棱台成两部分的体积之比是__________.三、解答题(每小题8分,共16分)7.(2011·福建高考)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.(1)求证:CE⊥平面PAD;(2)若PA=AB=1,AD=3,CD=,∠CDA=45°,求四棱锥P-ABCD的体积.8.(2012·揭阳模拟)已知如图,在平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=求四棱锥F-ABCD的体积.【挑战能力】(10分)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(1)求证:BM∥平面ADEF;(2)求几何体ABCDEF的体积和表面积.2答案解析1.【解析】选B.该几何体由两个相同的三棱柱组成,每个三棱柱的底面为直角三角形,且S底面=×2×=,高h=4.∴V=2××4=12.2.【解析】选D.设原正方体的棱长为a,若表面积增为原来的2倍,则棱长增为a.体积变为原来的()3=2倍.3.【解题指南】由三视图可知,几何体底面是两直角边分别是1和2的直角三角形,高为3的棱锥.【解析】选A.三棱锥的体积为4.【解析】选D.S上底=S下底=V=5.【解析】易知该四棱锥底面为正方形,高为2,∴V=答案:6.【解析】设棱台高为2h,上底面面积为S,则下底面面积为9S,中截面面积为4S,答案:【误区警示】注意此题中棱台上、下底面面积之比为1∶9,容易和边长的比混为一谈.另外还要注意公式的正确运用.7.【解析】(1)因为PA⊥平面ABCD,CE平面ABCD,所以PA⊥CE.因为AB⊥AD,CE∥AB,所以CE⊥AD.又PA∩AD=A,所以CE⊥平面PAD.(2)由(1)可知CE⊥AD.在Rt△CED中,DE=CD·cos45°=1,CE=CD·sin45°=1.3又因为AB=CE=1,AB∥CE,所以四边形ABCE为矩形.所以S四边形ABCD=S矩形ABCE+S△ECD=又PA⊥平面ABCD,PA=1,所以V四棱锥P-ABCD=S四边形ABCD·PA=8.【解析】(1)∵EF∥AD,AD∥BC,∴EF∥BC且EF=AD=BC,∴四边形EFBC是平行四边形,∴H为FC的中点.又∵G是FD的中点,∴HG∥CD,∵HG平面CDE,CD平面CDE,∴GH∥平面CDE.(2)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.∵BC=6,∴FA=6.又∵CD=2,DB=CD2+DB2=BC2,∴BD⊥CD,∴S□ABCD=CD·BD=∴VF-ABCD=S□ABCD·FA=××6=【一题多解】(1)连接EA,∵ADEF是正方形,∴G是AE的中点,∴在△EAB中,GH∥AB.又∵AB∥CD,∴GH∥CD,∵HG平面CDE,CD平面CDE,∴GH∥平面CDE.【挑战能力】【解析】(1)取DE的中点G,连接MG,AG.∵MG∥AB∥DC且AB=MG,∴四边形ABMG为平行四边形,∴BM∥AG.又∵BM平面ADEF,AG平面ADEF.∴BM∥平面ADEF.(2)体积:VABCDEF=VB-ADEF+VE-BDC=表面积:S表=S四边形ABCD+S四边形ADEF+S△ABF+S△DCE+S△BFE+S△BCE4=6+4+2+4+5