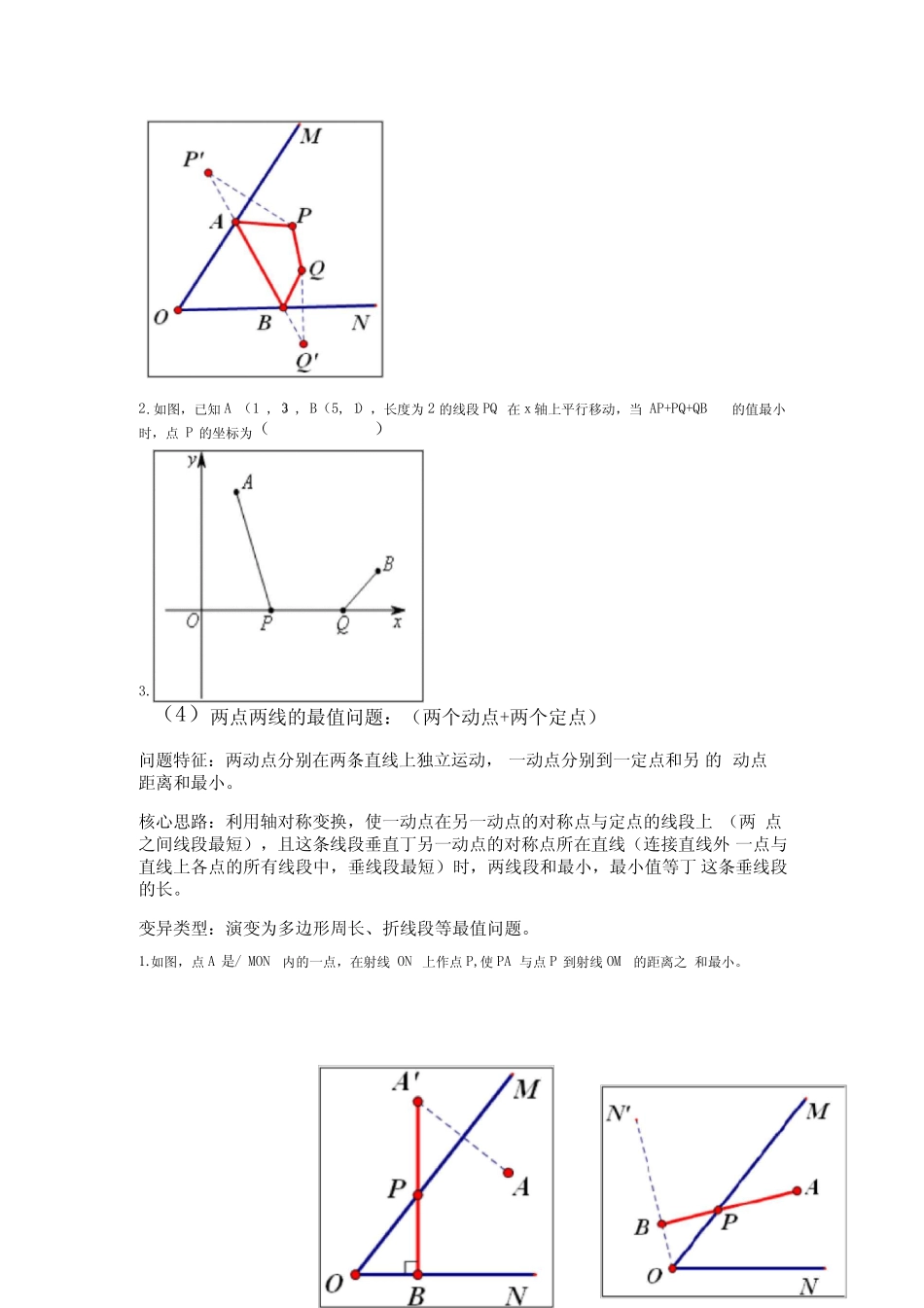
轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个:(1)两点之间线段最短;(2)三角形两边之和大丁第三边;(3)垂线段最短。初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,点两线三类线段和的最值问题。下面对三类线段和的最值问题进行分析、讨论。(1)两点一线的最值问题:(两个定点+一个动点)问题特征:已知两个定点位丁一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关丁直线的对称点,连结这个对称点与另一定点,交直线丁一点,交点即为动点满足最值的位置。方法:1.定点过动点所在直线做对称。2.连结对称点与另一个定点,则直线段长度就是我们所求。变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上1.如图,直线10和M的同侧两点A、B,在直线@上求作一点P,使PA+PB最小。(2)一点两线的最值问题:(两个动点+一个定点)问题特征:已知一个定点位丁平面内两相交直线之间,分别在两直线上确定两个2.如图,点A是ZMON夕卜的一点,在射线和最小。OM上作点P,使PA与点P到射线ON的距离之动点使线段和最短。核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关丁两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。变异类型:1.如图,点P是ZMON内的一点,分别在OM,ON上作点A,B。使^RAB的周长最小。(3)两点两线的最值问题:(两个动点+两个定点)问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。核心思路:用平■移方法,可把两动点变成一个动点,转化为“两个定点和一个动点”类型来解。变异类型:1.如图,点P,Q为/MON内的两点,分别在OM,ON上作点A,B。使四边形PAQB的周长最小。动点2.如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,当AP+PQ+QB的值最小时,点P的坐标为()(4)两点两线的最值问题:(两个动点+两个定点)问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另的距离和最小。核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最短),且这条线段垂直丁另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线段中,垂线段最短)时,两线段和最小,最小值等丁这条垂线段的长。变异类型:演变为多边形周长、折线段等最值问题。1.如图,点A是/MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。3.、常见题目求EM+EC的最小值。Parti、三角形1.如图,在等边△ABC中,AB=6,AD±BC,E是AC上的一点,M是AD上的一点,且AE=2,2.如图,在锐角△ABC中,AB=42,/BAC=45°,/BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,贝UBM+MN的最小值是。3.如图,△ABC中,AB=2,ZBAC=30°,若在AC、AB上各取一点M、N,使BM+MN的值最小,则这个最小值。A.[2/|B.国司C.33.接Part2、正方形1.如图,正方形ABCD的边长为8,M在DC上,丐DM=2,N是AC上的一动点,DN+MN的最小值为。即在直线AC上求一点N,使DN+MN最小。2.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()在边长为2cm的正方形ABCD中,点Q为BC边的中点,PB、PQ,则^PBQ周长的最小值为cmQ4.如图,四边形ABCD是正方形,求PC+PE的最小值;BPart3、矩形1.如图,若四边形ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PD的最小值;Part4、菱形1.如图,若四边形ABCD是菱形,AB=10cm,ZABC=45°,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值;一次函数y=kx+b的图象与l...