四阶龙格-库塔(R-K)方法求常微分方程VIP免费

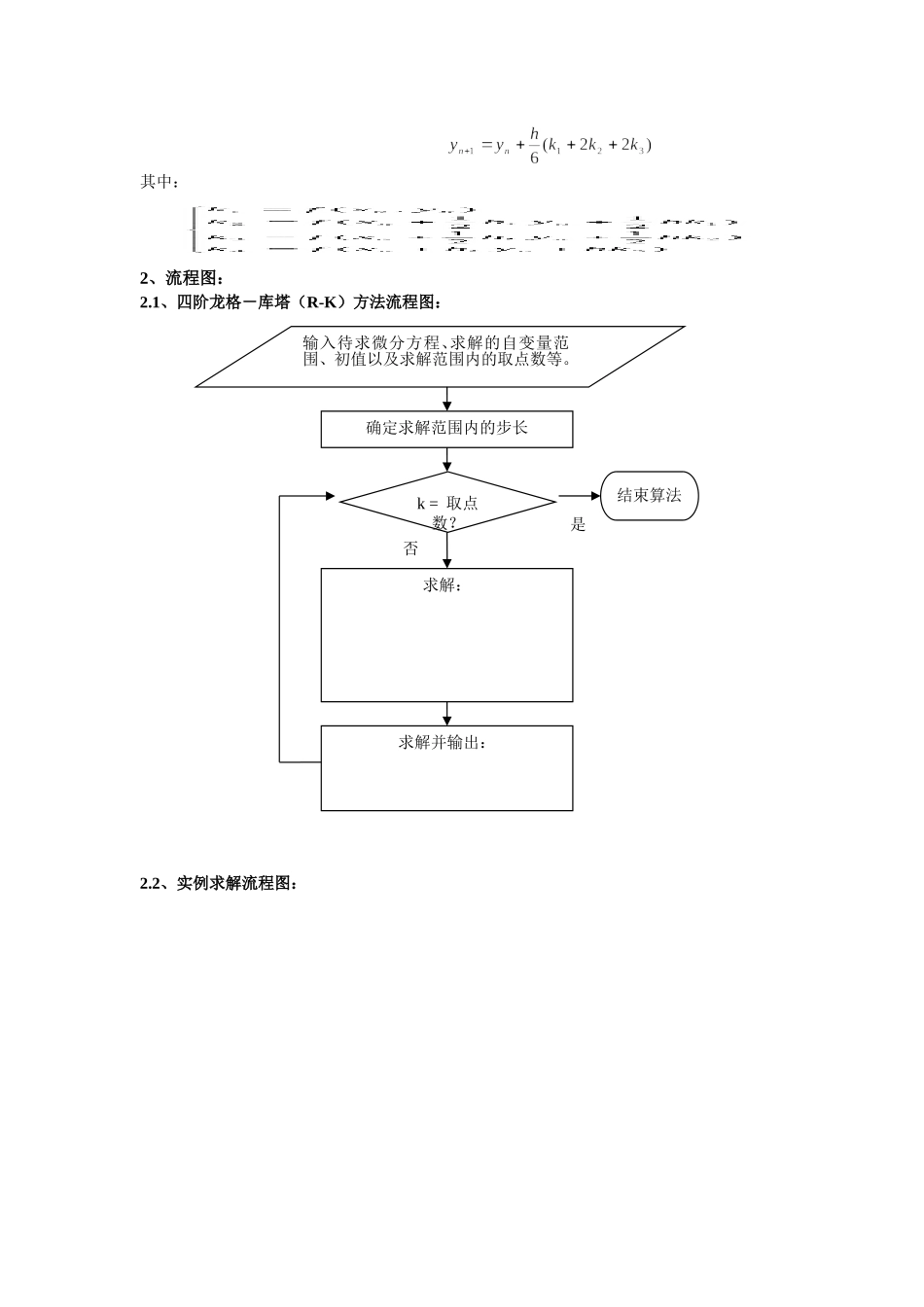
中南大学MATLAB程序设计实践材料科学与工程学院2013年3月26日一、编程实现“四阶龙格－库塔（R-K）方法求常微分方程”，并举一例应用之。【实例】采用龙格-库塔法求微分方程：1、算法说明：在龙格-库塔法中，四阶龙格-库塔法的局部截断误差约为o(h5)，被广泛应用于解微分方程的初值问题。其算法公式为：其中：2、流程图：2.1、四阶龙格－库塔（R-K）方法流程图：2.2、实例求解流程图：输入待求微分方程、求解的自变量范围、初值以及求解范围内的取点数等。确定求解范围内的步长k=取点数？否求解：求解并输出：是结束算法3、源程序代码3.1、四阶龙格－库塔（R-K）方法源程序：function[x,y]=MyRunge_Kutta(fun,x0,xt,y0,PointNum,varargin)%Runge-Kutta方法解微分方程形为y'(t)=f(x,y(x))%此程序可解高阶的微分方程。只要将其形式写为上述微分方程的向量形式%函数f(x,y):fun%自变量的初值和终值：x0,xt%y0表示函数在x0处的值，输入初值为列向量形式%自变量在[x0,xt]上取的点数：PointNum%varargin为可输入项，可传适当参数给函数f(x,y)%x：所取的点的x值%y：对应点上的函数值ifnargin<4|PointNum<=0PointNum=100;endifnargin<3y0=0;endy(1,:)=y0(:)';%初值存为行向量形式h=(xt-x0)/(PointNum-1);%计算步长x=x0+[0:(PointNum-1)]'*h;%得x向量值fork=1:(PointNum)%迭代计算输入求解的自变量范围求出待求简单微分方程的真值解用MATLAB自带函数ode23求解待求微分方程结束用自编函数四阶龙格－库塔（R-K）方法求解待求微分方程开始f1=h*feval(fun,x(k),y(k,:),varargin{:});f1=f1(:)';%得公式k1f2=h*feval(fun,x(k)+h/2,y(k,:)+f1/2,varargin{:});f2=f2(:)';%得公式k2f3=h*feval(fun,x(k)+h/2,y(k,:)+f2/2,varargin{:});f3=f3(:)';%得公式k3f4=h*feval(fun,x(k)+h,y(k,:)+f3,varargin{:});f4=f4(:)';%得公式k4y(k+1,:)=y(k,:)+(f1+2*(f2+f3)+f4)/6;%得y(n+1)end3.2、实例求解源程序：%运行四阶R-K法clear,clc%清除内存中的变量x0=0;xt=2;Num=100;h=(xt-x0)/(Num-1);x=x0+[0:Num]*h;a=1;yt=1-exp(-a*x);%真值解fun=inline('-y+1','x','y');%用inline构造函数f(x,y)y0=0;%设定函数初值PointNum=5;%设定取点数[x1,y1]=ode23(fun,[0,2],0);[xr,yr]=MyRunge_Kutta(fun,x0,xt,y0,PointNum);MyRunge_Kutta_x=xr'MyRunge_Kutta_y=yr'plot(x,yt,'k',x1,y1,'b--',xr,yr,'r-')legend('真值','ode23','Rung-Kutta法解',2)holdonplot(x1,y1,'bo',xr,yr,'r*')4、程序运行结果：MyRunge_Kutta_x=00.50001.00001.50002.0000MyRunge_Kutta_y=00.39320.63180.77660.8645二、变成解决以下科学计算问题：（一）[例7-2-4]材料力学复杂应力状态的分析——Moore圆。1、程序说明：利用平面应力状态下斜截面应力的一般公式，画出任意平面应力状态下的应力圆（Moore圆），求出相应平面应力状态下的主应力（、），并求出该应力状态下任意方位角的斜截面上的应力、。xyyxyxyxxyxy2、程序流程图：3、程序代码：clear;clc;Sx=input('Sigma_x(MPa)=');%输入该应力状态下的各应力值Sy=input('Sigma_y(MPa)=');Txy=input('Tau_xy(MPa)=');a=linspace(0,pi,100);%等分半圆周角Sa=(Sx+Sy)/2;Sd=(Sx-Sy)/2;Sigma=Sa+Sd*cos(2*a)-Txy*sin(2*a);%应力圆一般方程Tau=Sd*sin(2*a)+Txy*cos(2*a);plot(Sigma,Tau,Sx,Txy,'.r',Sy,-Txy,'.r');%画出应力圆，标出该应力状态下各应力参数line([Sx,Sy],[Txy,-Txy]);axisequal;%控制各坐标轴的分度使其相等——使应力圆变圆开始输入待求应力状态的参数画出应力圆求某一方向角截面上的应力?输入方向角求出相应正应力、切应力是否得出该应力状态下的主应力求出主应力平面方向角结束title('应力圆');xlabel('正应力（MPa）');ylabel('剪应力（MPa）');text(Sx,Txy,'A');text(Sy,-Txy,'B');Smax=max(Sigma);Smin=min(Sigma);Tmax=max(Tau);Tmin=min(Tau);b=axis;%提取坐标轴边界ps_array.Color='k';%控制坐标轴颜色为黑色line([b(1),b(2)],[0,0],ps_array);%调整坐标轴line([0,0],[b(3),b(4)],ps_array);b=axis;%提取坐标轴边界line([b(1),b(2)],[0,0],ps_array);%画出x...