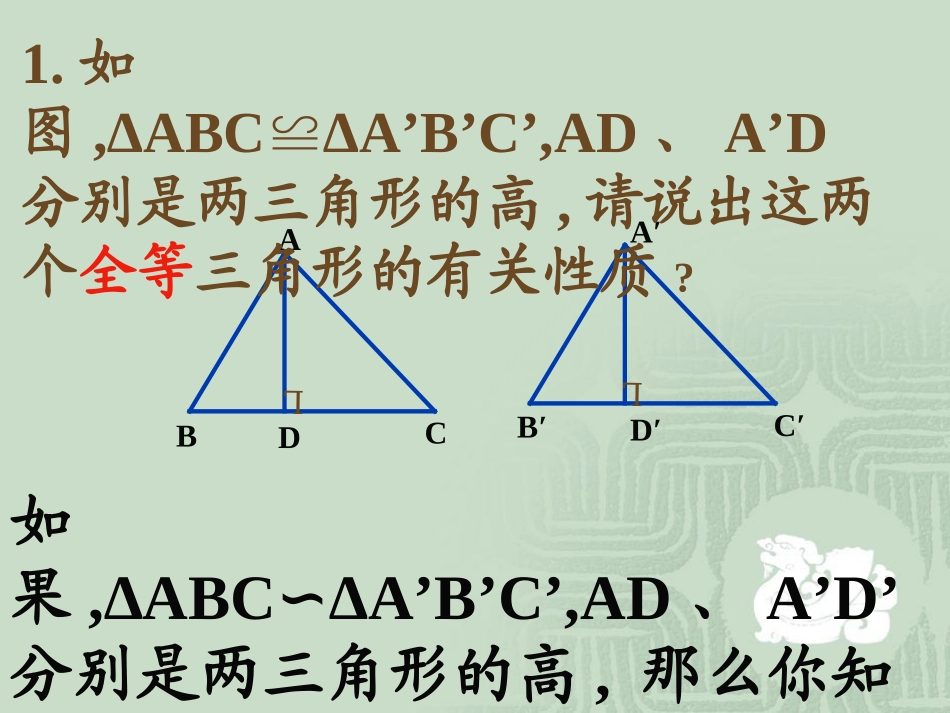
ⅬABCDⅬA′B′C′D′1.如图,∆ABC∆A’B’C’,AD≌、A’D分别是两三角形的高,请说出这两个全等三角形的有关性质?如果,∆ABC∆A’B’C’,AD∽、A’D’分别是两三角形的高,那么你知道他们有什么性质吗?某技术工人准备按照比例尺3:4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.ABCDA′B′C′D′ABCDA′B′C′D′43''''''ACCACBBCBAAB''CBBC''ACCA1)各等于多少?''BAABABCDA′B′C′D′2)ABC△与△A′B′C′相似吗?如果相似请说明理由,并指出它们的相似比.43''''''ACCACBBCBAAB因为△ABC∽△A′B′C′ABCDB′A′C′D′3)图中还有相似三角形吗?(简单说明理由)△ACD∽△A′C′D′△BCD∽△B′C′D′ABCDA′B′C′D′4)''DCCD等与多少?你是怎么做的?43''DCCD已知△ABC∽△A′B′C′.ABC△与△A′B′C′他们的相似比为k1)如果CD和C’D’是它们的对应高,那么等与多少?''DCCD2)如果CE和C’E’是它们的角平分线,那么等与多少?''ECCE?''FCCF中位线是CF和C’F’相似三角形对应高的比与相似比的关系及其理由如图∵△ABCDEF.B=E.∽△∴∠∠又∵∠AMB=DNE=90∠0.∴△AMBDNE.∽△(两角对应相等的两个三角形相似).相似三角形对应高的比等于相似比.理由是:(相似三角形对应边成比例).ABCMDEFN.DEABDNAM相似三角形对应角平分线的比与相似比的关系及其理由如图∵△ABCDEF.∽△∴∠B=E,BAC=EDF.∠∠∠又∵AM,DN分别是∠BAC和∠EDF的角平分线.∴∠BAM=EDN.∠∴△AMBDNE.∽△(两角对应相等的两个三角形相似).相似三角形对应角平分线的比等于相似比.理由是:(相似三角形对应边成比例).ABCMDEFN.DEABDNAM相似三角形对应中线的比与相似比的关系及其理由如图∵△ABCDEF.∽△∴∠B=E,∠相似三角形对应中线的比等于相似比.理由是:(相似三角形对应边成比例).ABCMDEFN.DEABDNAM.EFBCDEAB又∵AM,DN分别是△ABC和△DEF的中线..EFBCENBM∴△AMBDNE.∽△(两边对应成比例且夹角相等的两个三角形相似)..ENBMDEAB且∠B=E.∠相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。相似三角形的性质例题欣赏P147如图所示,在等腰△ABC中,底边BC=60cm,高AD=40cm,四边形PQRS是正方形.(1).ASR△与△ABC相似吗?为什么?(2).求正方形PQRS的边长.解:(1)ASRABC.△∽△理由是:(2).由(1)可知,ASRABC.△∽△四边形PQRS是正方形RSBC∥∠ASR=B∠∠ARS=C∠△ASRABC.∽△.BCSRADAE设正方形PQRS的边长为xcm,则AE=(40-x)cm,.604040xx解得,x=24.所以正方形PQRS的边长为24cm.ABCSREPDQ(相似三角形对应高的比等于相似比)1.如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是,对应边上的中线的比是______。2.如果两相似三角形的对应边上的中线的比为1:2,那么对应边上高的比是____。3.△ABC与△A'B'C'的相似比为1:3,若B’C’=15cm,则BC=_____。2:32:31:25cm4.△ABC与△A‘B’C‘的相似比为3:4,若BC边上的高AD=12cm,则B‘C’边上的高A‘D’=。5.△ABC与△A’B’C’的相似比为1:5,如果A’C’边上的中线B’D’=20cm,则AC边上的中线BD=____。6.如图△ABCA’B’C’∽△,对应中线AD=6cm,A’D’=10cm,若BC=4.2cm,则B’C′=______。4cm7cm16cm相似三角形的性质(特别注意“对应”二字)对应角相等对应边成比例对应高的比、对应中线的比、对应角平分线的比都等于相似比.ⅬABCDEFⅬA′B′C′D′E'F'