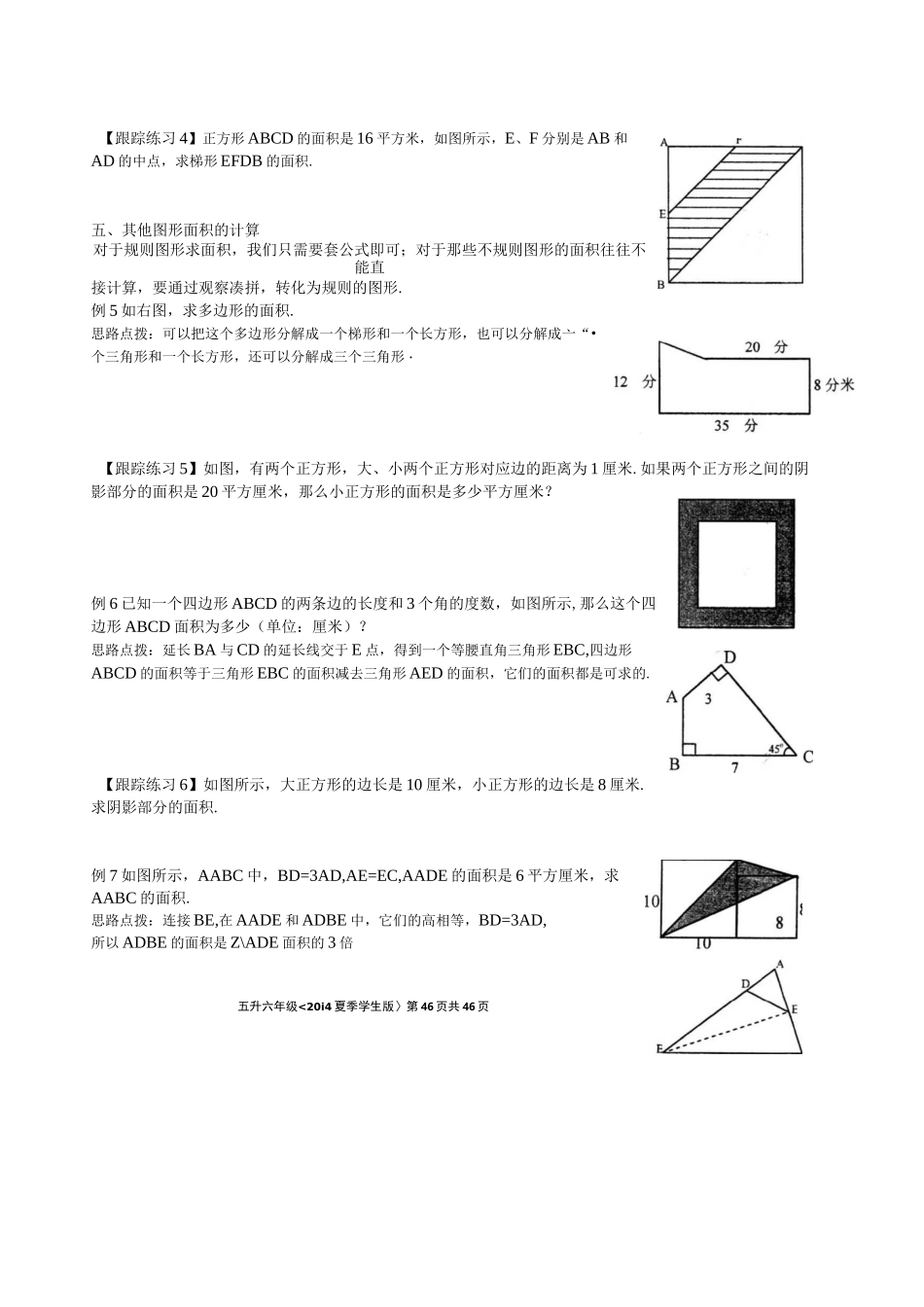
五升六年级<2014夏季学生版〉第44页共44页第8讲几何图形面积的计算知识对接小升初必备①求面积公式:三角形面积=底><高*2平行四边形面积=底乂高梯形面积=(上底+下底)X高一2长方形面积=长乂宽正方形面积=边长X边长菱形面积=两条对角线乘积的一半②课堂疑难知识点:(1)根据面积公式对规则图形求面积值.(2)通过分解、割补等方法求组合图形的面积.竞赛拓展解答几何图形的面积要注意下面几点:1•切实拿握有关的概念、公式,建立初步的空间观念.2•仔细观察、分析,要看组合图形是由哪几个基本图形组成的,它们之间有什么关系,有没有公共部分.3•解纟6合图形问题,常用分解法、割补法、等量代换法.4•添辅助线,有助于我们把隐蔽条件找出来,有利于使要求的问题很快得到解决.此外,还可把几何图形中的部分图形进行平移、翻折、旋转,使问题化难为易.思维对接小升初例题一、三角形的面积计算三角形等高,面积的比等于底边的比;三角形等底,面积的比等于高的比.例1如右图是平行四边形,面积是48平方厘米,求阴影部分的面积.思路点拨:按“底=面积*高”求出底,再求阴影部分三角形的底,最后按公式求出阴影部分的面积.五升六年级<2014夏季学生版〉第44页共45页【跟踪练习1】如图,已知直角三角形ABC中,AC=6厘米,BC=8厘米,AB=10厘米,将AC对折到斜边AB上去,C落在斜边AB±的点E处,那么图中阴影部分的面积是多少平方厘米?二、长方形与正方形面积的计算掌握并能熟练运用长方形、•正方形的面积公式.对于那些不能直接利用公式的图形,我们可以采用“割补”、“平移”、“旋转”等方法,使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答.例2如图所示,在正方形ABCD中,三角形ABE的面积是8平方厘米,4它是三角形DEC的面积的;,求正方形ABCD的面积.思路点拨:过点E作BC的垂线交AD于F,在长方形ABEF中AE是对角线,AABE的面积等于AAEF的面积等于8平方厘米,同理,ADEC的面积等于△EDF的面积.【跟踪练习2】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有两道红条,如图所示,红条宽都是2厘米,问这条手帕白色部分的面积是多少平方厘米?三、平行四边形面积的计算平行四边形面积=底><高,注意与三角形面积之间的关系,会利用公式变形求底或高.例3在一块平行四边形的稻田里,底120米,高90米,共收稻谷8.5吨,平均每公顷收稻谷多少千克?(得数保留整数)思路点拨:要求平均每公顷收稻谷多少千克,先算出这块稻田的面积是多少平方米,最后求出平均每公顷收稻谷多少千克.【跟踪练习3】如图,已知平行四边形的面积和底•求高.四、梯形面积的计算求梯形的面积时,可以分成几块面积再相加,也可以用公式:梯形面积=(上底+下底)例4有一个等腰梯形,底角为45°,上底为8厘米,下底为12厘米,求这个梯形的形面积是多少平方厘米?思路点拨:利用两个底角为45。求出高.ABCD【跟踪练习4】正方形ABCD的面积是16平方米,如图所示,E、F分别是AB和AD的中点,求梯形EFDB的面积.五、其他图形面积的计算对于规则图形求面积,我们只需要套公式即可;对于那些不规则图形的面积往往不能直接计算,要通过观察凑拼,转化为规则的图形.例5如右图,求多边形的面积.思路点拨:可以把这个多边形分解成一个梯形和一个长方形,也可以分解成亠“•个三角形和一个长方形,还可以分解成三个三角形・【跟踪练习5】如图,有两个正方形,大、小两个正方形对应边的距离为1厘米.如果两个正方形之间的阴影部分的面积是20平方厘米,那么小正方形的面积是多少平方厘米?例6已知一个四边形ABCD的两条边的长度和3个角的度数,如图所示,那么这个四边形ABCD面积为多少(单位:厘米)?思路点拨:延长BA与CD的延长线交于E点,得到一个等腰直角三角形EBC,四边形ABCD的面积等于三角形EBC的面积减去三角形AED的面积,它们的面积都是可求的.【跟踪练习6】如图所示,大正方形的边长是10厘米,小正方形的边长是8厘米.求阴影部分的面积.例7如图所示,AABC中,BD=3AD,AE=EC,AADE的面积是6平方厘米,求AABC的面积.思路点拨:连接BE,在AADE和ADBE中,它们的高相等,BD=3AD,所以ADBE的面积是Z\ADE面积的3倍五升六年级<20i...