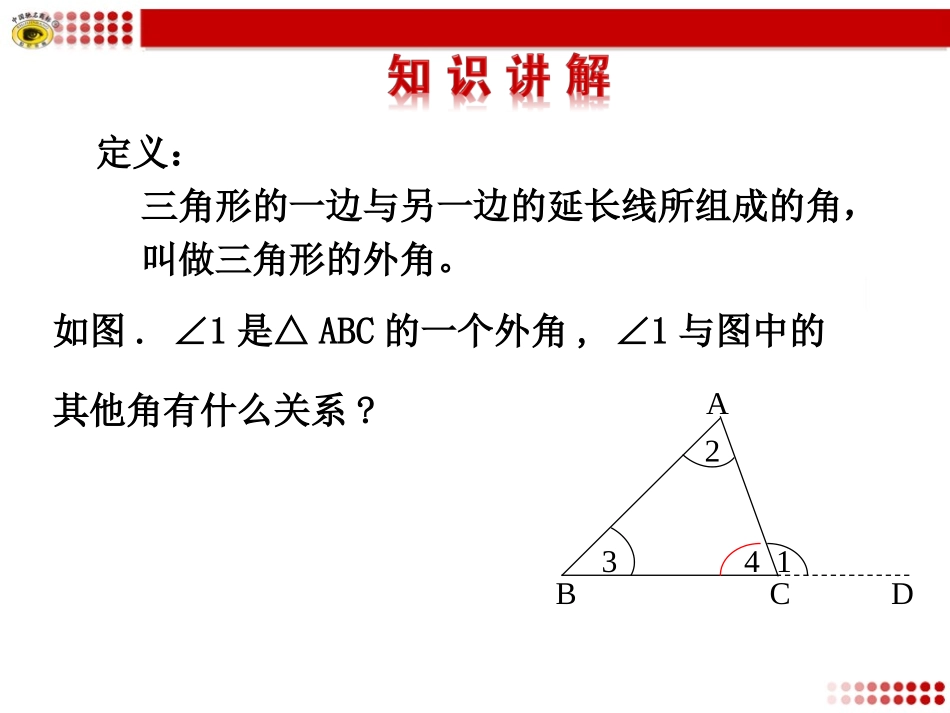
5三角形内角和定理第2课时如图.∠1是△ABC的一个外角,∠1与图中的其他角有什么关系?ABCD1234定义:三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。用文字表述为:三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.在这里,我们通过三角形的内角和定理直接推导出两个新定理.像这样,由一个基本事实或定理直接推出的定理,叫做这个基本事实或定理的推论.推论可以当做定理使用.三角形内角和定理的推论:定理:三角形的一个外角等于和它不相邻的两个内角的和.定理:三角形的一个外角大于任何一个和它不相邻的内角.ABCD1234ABCD1234△ABC中:∠1=∠2+∠3;∠1>∠2,∠1>∠3.这个结论以后可以直接运用.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于()A.60°B.70°C.80°D.90°ABCD1.已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.求:∠B和∠ACB的大小.【跟踪训练】例1已知:如图,在△ABC中,AD平分外角∠EAC,∠B=∠C.求证:AD∥BC.ACDBE【例题】例2已知:如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.求证:∠1>∠2.CABF1345ED2【例题】2.已知:如图所示.求证:∠BDC>∠A.BCADE4.已知:如图,已知CE为△ABC外角∠ACD的平分线,CE交BA的延长线于点E,求证:∠BAC>∠B.2.如图,AB∥CD,则下列说法正确的是()A.∠3=2∠1+∠2B.∠3=2∠1-∠2C.∠3=∠1+∠2D.∠3=180°-∠1-∠2理解几何命题证明的方法,步骤,格式及注意事项.三角形内角和定理.三角形三个内角的和等于180°.△ABC中,∠A+∠B+∠C=180°.推论1:三角形的一个外角等于和它不相邻的两个内角的和.推论2:三角形的一个外角大于任何一个和它不相邻的内角.