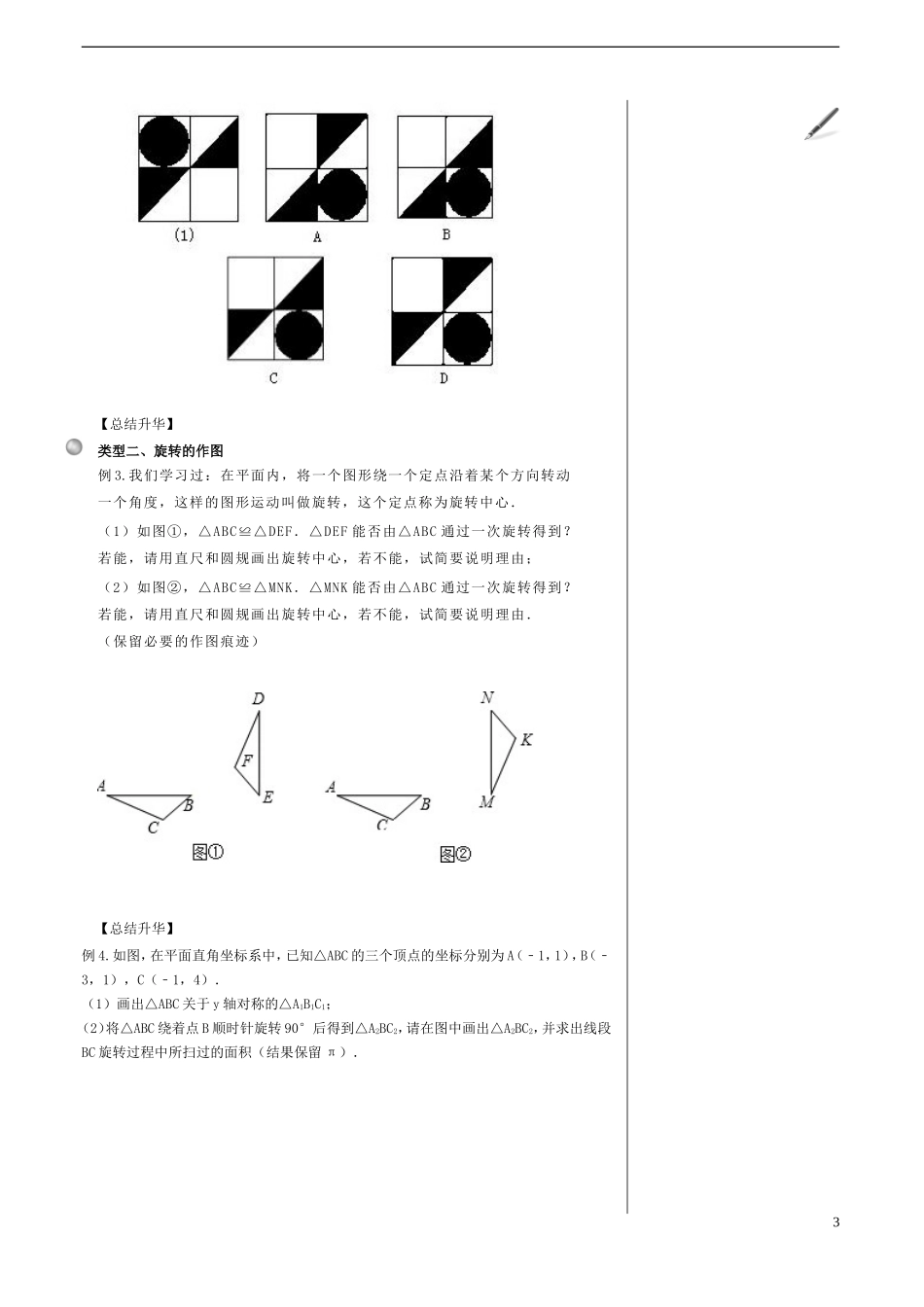
图形的旋转一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:掌握旋转的概念,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;能够按要求作出简单平面图形旋转后的图形,并能利用旋转进行简单的图案设计.学习策略:类比轴对称变换来学习本节内容;掌握基本概念是学好图形旋转的基础.二、学习与应用1.如果一个图形沿着某条直线折叠,直线两旁的部分能够,那么这个图形叫做轴对称图形,这条直线叫做这个图形的.2.关于x轴对称的两个点,坐标相同,坐标相反;关于y轴对称的两个点坐标相同,坐标相反.要点一、旋转的概念将一个图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.定点称为,旋转的角度称为.要点二、旋转的性质一个图形和它经过旋转所得到的图形中:(1)对应点到旋转中心的距离;1“凡事预则立,不预则废”.科学地预习才能使我们上课听讲更有目的性和针对性.我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记.要点梳理——预习和课堂学习认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习.课堂笔记或者其它补充填在右栏.知识回顾——复习学习新知识之前,看看你的知识贮备过关了吗?(2)两组对应点分别与旋转中心连线所成的相等.要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.要点三、旋转的作图在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键点沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.要点诠释:作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;(4)连接所得到的各对应点.类型一、旋转的概念与性质例1.如图,把四边形AOBC绕点O旋转得到四边形DOEF.在这个旋转过程中(1)旋转中心是谁?(2)旋转方向如何?(3)经过旋转,点A、B的对应点分别是谁?(4)图中哪个角是旋转角?(5)四边形AOBC与四边形DOEF的形状、大小有何关系?(6)AO与DO的长度有什么关系?BO与EO呢?(7)∠AOD与∠BOE的大小有什么关系?【总结升华】举一反三【变式】如图所示:O为正三角形ABC的中心.你能用旋转的方法将△ABC分成面积相等的三部分吗?如果能,设计出分割方案,并画出示意图.例2.如图,将图(1)中的正方形图案绕中心旋转180°后,得到的图案是()2典型例题——自主学习认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三.课堂笔记或者其它补充填在右栏.【总结升华】类型二、旋转的作图例3.我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心.(1)如图①,△ABC≌△DEF.△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由;(2)如图②,△ABC≌△MNK.△MNK能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.(保留必要的作图痕迹)【总结升华】例4.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).(1)画出△ABC关于y轴对称的△A1B1C1;(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).3举一反三【变式1】如图,画出绕点逆时针旋转所得到的图形.【变式2】阅读材料:如图(一),在已建立直角坐标系的方格纸中,图形①的顶点为A、B、C,要将它变换到图④(变换过程中图形的顶点必须在格点上,且不能超出方格纸的边界).例如:将图形①作如下变换(如图二).第一步:平移,使点C(6,6)移至点(4,3),得图②;第二步:旋转,绕着点(4,3)旋转180°,得图③;第三步:平移,使点(4,3)移至点O(0,0),得图④.则图形①被变换到了图④.解决问题:...