第十章 随机过程及其统计描述VIP免费

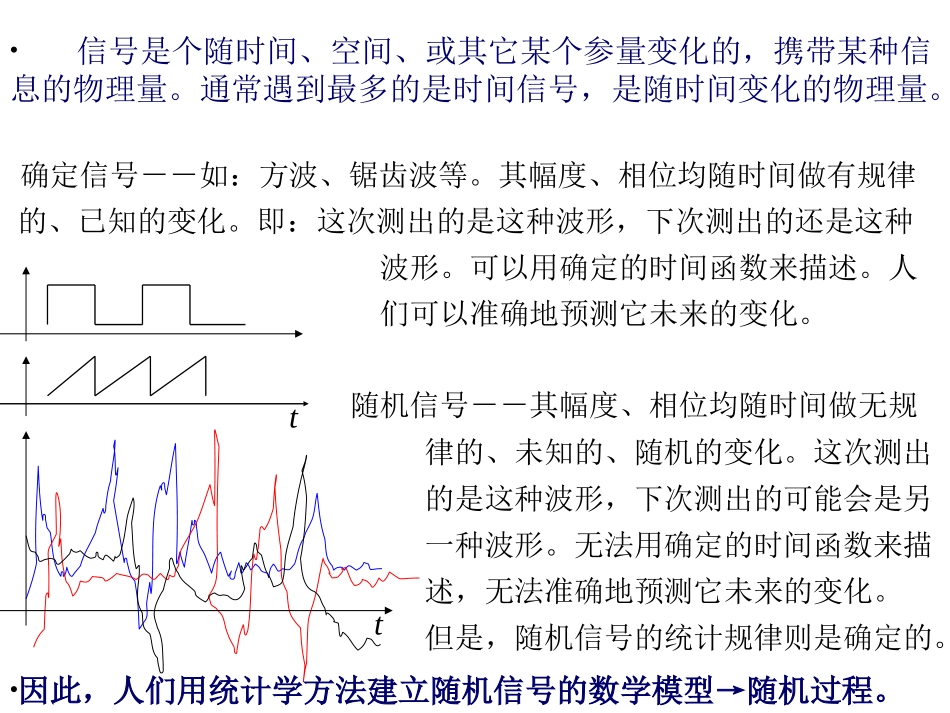
随机过程随机过程关键词：随机过程状态和状态空间样本函数有限维分布函数均值函数方差函数自相关函数自协方差函数互相关函数互协方差函数正态过程独立增量过程泊松过程维纳过程第十章随机过程及其统计描述tt确定信号－－如：方波、锯齿波等。其幅度、相位均随时间做有规律的、已知的变化。即：这次测出的是这种波形，下次测出的还是这种波形。可以用确定的时间函数来描述。人们可以准确地预测它未来的变化。随机信号－－其幅度、相位均随时间做无规律的、未知的、随机的变化。这次测出的是这种波形，下次测出的可能会是另一种波形。无法用确定的时间函数来描述，无法准确地预测它未来的变化。但是，随机信号的统计规律则是确定的。•信号是个随时间、空间、或其它某个参量变化的，携带某种信息的物理量。通常遇到最多的是时间信号，是随时间变化的物理量。•因此，人们用统计学方法建立随机信号的数学模型→随机过程。下面由一个试验实例来建立随机过程的概念。举例：在相同条件下，对同一雷达接收机的内部噪声电压（或电流）经过大量的重复测试后，设观测到的所有的可能结果有m种，记录下m个不相同的波形。1km10intttt111(,)(,)()iXtXtxt(,)(,)()kikkXtXtxt(,)(,)()mimmXtXtxt()iXtS.},),,({,),(,.},),,({,是随机过程则称是一个随机变量若此函数对任意固定的二元函数上的和为定义在是一个无限实数集设TtStXtXTtTSTtStXT定义：这里对每一个tT,X(t)是一随机变量.T叫做参数集.常把t看作为时间,称X(t)为时刻t时过程的状态,而X(t1)=x(实数)说成是t=t1时过程处于状态x,对于一切tT,X(t)所有可能取的一切值的全体称为随机过程的状态空间.t固定，变化：X(ti,ζ)随机变量（状态）。t固定，固定：X(ti,ζk)一个确定的值。t变化，固定：X(t,ζk)确定的时间函数(随机过程的样本函数）t变化，变化：X(t,ζ)随机过程（一族时间函数的总体，或随时间变化的随机变量）下标i和k，分别表示确定的某个时刻i和确定的某个样本k。对随机过程而言：).(),(tXtX简记为今后将一般，随机变量写成:X,Y,Z。随机过程写成:X(t),Y(t),Z(t)样本函数写成:x(t),y(t),z(t)或X1(t)……Xn(t)例1：抛掷一枚硬币的试验，样本空间是S={H,T}，现定义：1(),()()2(),,costHXttPHPTtTXtt当出现，其中当出现则是一随机过程。,()tXtcostt解：对任意固定的是随机变量，取值为和1234()Xt1()Xt2()Xtt1(())(())2PXtcostPXtt12(),()XtcostXtt此随机过程的样本函数只有两个，即2()(),,,(0,2),()(),(0,2),()(),XtcostttXtcostxtcost例：考虑式中和是正常数,是在上服从均匀分布的随机变量,这是一个随机过程。对每一固定的时刻是随机变量的函数,从而也是随机变量。它的状态空间是[-].在内随机取一数相应的就得到一个样本函数这族样本函数的差异在于它们相位的不同,故这一过程称为随机相位正弦波。3(),[0,1]()()[0,1]().XtVcosttVXttXtVcostVcostvxtvcost例：设其中是常数；在上服从均匀分布,则是一个随机过程。对每一固定的，是随机变量乘以常数，故也是随机变量,对上随机变量取一值,就得到相应的一个样本函数4120()0,0()(),00,1,2,.XtttXtXtt例：设某城市的急救中心电话台迟早会接到用户的呼叫。以表示时间间隔内接到的呼叫次数，它是一个随机变量，且对于不同的，是不同的随机变量，于是是一随机过程，且它的状态空间是1t2t3t4t'1t'2t'4t'3t14231()xt2()xt()xtt例5：考虑抛掷一颗骰子的试验：16(1)(1)1,2,(),1,2,3,4,5,6,1nnnnXnnnXPXiiXn设是第次抛掷的点数，对于的不同值，是随机变量，服从相同的分布，因而构成一随机过程，称为伯努利过程或伯努利随机序列,它的状态空间为1,2,3,4,5,6。(2),11,2,3,4,5,6nnYnYn设是前次抛掷中出现的最大点数,也是一随机过程，它的状态空间仍是。下面分别给出它们的一条样本函数：n87654321nx321654nx(1)(2)n87654321ny...