第一章 整式的乘除回顾思考VIP免费

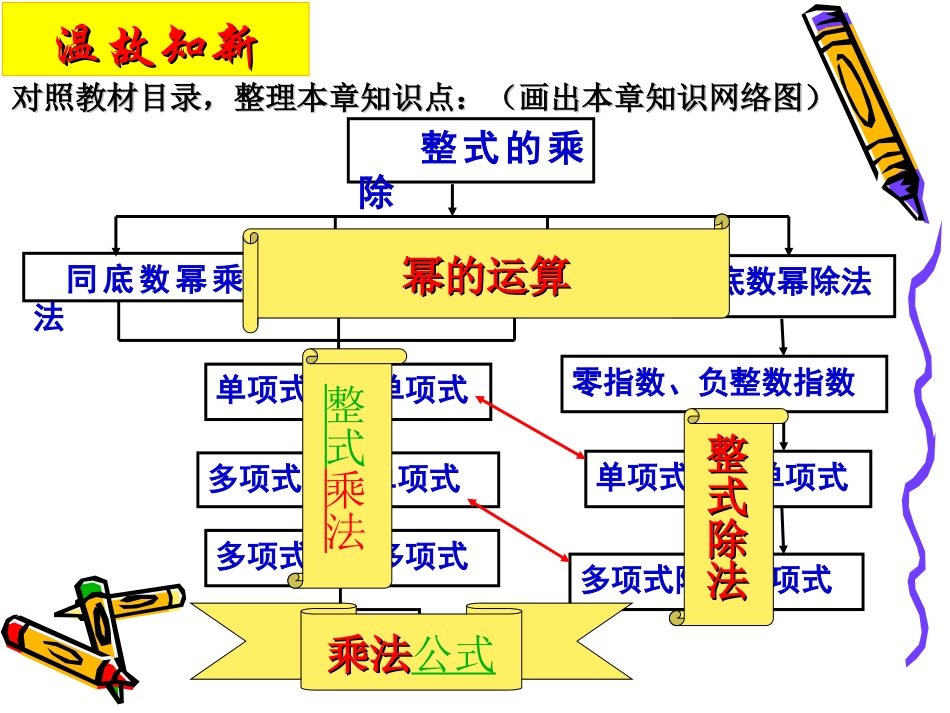
第一章整式的乘除第一章整式的乘除回顾与思考回顾与思考授课吴逢军授课吴逢军学习目标学习目标22、掌握整式的运算在实际问题中的应用。、掌握整式的运算在实际问题中的应用。11、掌握幂的运算法则，并会逆向运用；、掌握幂的运算法则，并会逆向运用；熟练运用乘法公式。熟练运用乘法公式。温故知新温故知新对照教材目录，整理本章知识点：（画出本章知识网络图）对照教材目录，整理本章知识点：（画出本章知识网络图）整式的乘除同底数幂乘法幂的乘方积的乘方同底数幂除法单项式乘以单项式零指数、负整数指数多项式乘以单项式单项式除以单项式多项式乘以多项式多项式除以单项式乘法公式幂的运算幂的运算整式乘法整式除法整式除法乘法乘法公式颗粒归仓颗粒归仓知识点法则简述注意同底数幂的乘法aman=am+n幂的乘方(am)n=amn积的乘方（ab)n=anbn底数不变指数相加a既可以是数，也可以是“式”底数不变指数相乘将积中每个因式分别乘方，再相乘不要漏乘积中每个因式，特别是符号问题公式的逆用(am)n=amn=(an)m同底数幂的除法am÷an=am－n底数不变指数相减a的取值范围特别要注意拓展知识：拓展知识：）0(10aa零指数幂零指数幂负指数幂负指数幂）0(11aaaappp()()()()()()()()()()××√√235223636532633224424432432153232333)().(102010.9.8)()().(76)2.(6)()().(5)(.4)(.3)(.22.1mmmaaaayxxyyxxxaaabbbxxxxxxxaaammmmm××××××××××××√√√√快问快答快问快答互帮互助互帮互助nnndcdc)()(221212(3)[27(3)]nn（4）（－3a3）2·a3＋（－a）2·a7－（5a3）3（3）（1）3225xx2233322yxyxyx（2）（5）方法小结：方法小结：先算积的乘方，再算幂的乘法，先算积的乘方，再算幂的乘法，最后算同底幂的乘除法最后算同底幂的乘除法先定符号再求值先定符号再求值若若mm为正整数，且为正整数，且xx2m2m＝＝33，，求求(3x3x3m3m)22－－13(xx22)2m2m的值的值例例22：：(逆用幂的运算公式)互帮互助互帮互助（3x3m）2－13（x2）2m解:=9x6m-13x4m x2m＝3=9(x2m)3-13(x2m)2∴原式=9×33-13×32=126颗粒归仓颗粒归仓单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变,作为积的因式。单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。单项式单项式××单项式单项式单项式单项式××多项式多项式多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加。多项式多项式××多项式多项式)31()43()32(2532cabcbca)6)(211012(3322xyyyxxy)2)(1()3)(2(yxyx)2)(2()2)(2(22xxxxxx互帮互助互帮互助（1）在与的积中不含和项，求p、q的值82pxxqxx323xx（2）先化简，再求值.已知，求：的值.3,21ba211212ababa例4：互帮互助互帮互助颗粒归仓颗粒归仓平方差公式:完全平方公式:(a+b)(a－b)=a2－b2（ab)2=a22ab+b2两个多项式的积，两两个多项式的积，两个多项式中个多项式中既有符号既有符号相同，又有符号相反相同，又有符号相反符号相同项符号相同项的平的平方方减去减去符号相反符号相反项的平方项的平方和和((差差))的平方的平方两项的平方和再加减两项的平方和再加减两项积的两倍，两项积的两倍，加减加减与两项的符号相同与两项的符号相同22)()(cbacba42212122224xxxxxxzyxzyx3232互帮互助互帮互助温馨提醒：温馨提醒：使用公式以后一定要记得加上括号使用公式以后一定要记得加上括号（（11）已知，）已知，求的值求的值2010)2012)(2014(aa22)2012()2014(aa（（22）当）当==，，==，，多项式有最小值，多项式有最小值，此时这个最小值是此时这个最小值是。。xy11249422yxyx例例66：：（（逆用完全平方公式）互帮互助互帮互助颗粒归仓颗粒归仓单项式单项式...