电路原理_5复阻抗、复导纳及其等效变换VIP免费

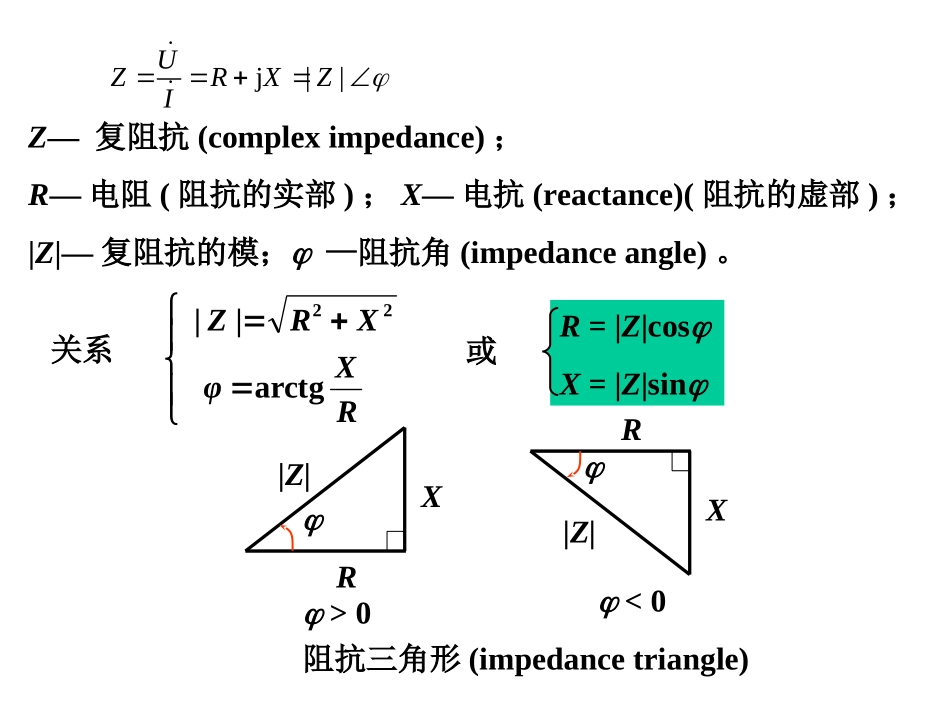
正弦电流电路的稳态分析正弦电流电路的稳态分析正弦电流电路的稳态分析正弦电流电路的稳态分析复阻抗、复导纳及其等效变换复阻抗、复导纳及其等效变换复阻抗、复导纳及其等效变换复阻抗、复导纳及其等效变换一、复阻抗Z正弦激励下，对于无独立源线性网络，可定义入端等效复阻抗纯电阻Z=R纯电感Z=jL=jXL纯电容Z=1/jC=jXCIZU+-无源线性IU+-)(j||defiuXRZIUZ)(j||defiuXRZIUZj||UZRXZIZ—复阻抗(compleximpedance)；R—电阻(阻抗的实部)；X—电抗(reactance)(阻抗的虚部)；|Z|—复阻抗的模；—阻抗角(impedanceangle)。关系arctg||22RXφXRZ或R=|Z|cosX=|Z|sin|Z|RX<0|Z|RX>0阻抗三角形(impedancetriangle)X>0，>0，电路为感性，u超前i；X<0，<0，电路为容性，i超前u；X=0，=0，电路为电阻性,i与u同相IUIUIUZ=R+jX=|Z|∠|Z|=U/I=u-i二、复导纳Y)'('||jdefuiYBGUIY)'('||jdefuiYBGUIY|Z|RX阻抗三角形|Y|GB导纳三角形对于上述的无独立源线性网络，同样可定义入端等效复导纳：CCLLRBCYBLYRYjj:jj1:/1:纯电容纯电感纯电阻IYU+-无源线性IU+-ZY1j||'iiuuIIIYψψGBYUUψUY—复导纳(complexadmittance)；G—电导(导纳的实部)；B—电纳(suspectance)(导纳的虚部)；|Y|—复导纳的模；—导纳角(admittanceangle)。关系arctg||22GB'BGY或G=|Y|cos'B=|Y|sin'导纳三角形(admittancetriangle)|Y|GB>0|Y|GB<0三、复阻抗和复导纳等效关系'||j||jφYBGYφZXRZ一般情况G1/RB1/X。若Z为感性，X>0，则B<0，即仍为感性。ZRjXGjBYφφZYXRXBXRRG',||1||,2222BGXRXRXRZYjjj1122同样，若由Y变为Z，则有：XRBGBGBGYZφZXRZφYBGYjjj11||j,'||j22',||1||,2222φφZYBGBXBGGRGjBYZRjX四、阻抗串联、并联的电路两个阻抗串联21ZZZ等效阻抗ZZ1Z2+++---U1U2UI两个阻抗并联2121212111ZZZZZZYYY等效导纳IY+-UZ1Z21I2IUZZZUUZZZU21222111,分压公式IZZZIIZZZI21122121,分流公式)(212121ZZIIZZIUUU2121ZZZZZ等效阻抗nkkZZ1等效阻抗n个阻抗串联nkkYY1等效导纳n个导纳并联),2,1(1nkUZZUnkkkk分压公式),2,1(1nkIYYInkkkk分流公式9.31j2028.6j10)9.31j20)(28.6j10(2121ZZZZZ例已知Z1=10+j6.28,Z2=20-j31.9,Z3=15+j15.7。Z1Z2Z3ab求Zab。Ω6.359.3156.18j89.2586.2j89.107.15j153abZZZ解5.4045.3961.5765.3713.3281.1186.2j89.10小结：小结：相量形式欧姆定理(2)Z是与u,i无关的复数。(3)根据Z、Y可确定无源二端网络的性能(4)一般情况Z、Y均是的函数返回首页返回首页无源线性IU+-ZIUIUZUYIUIY(1)