函数展开成幂级数VIP免费

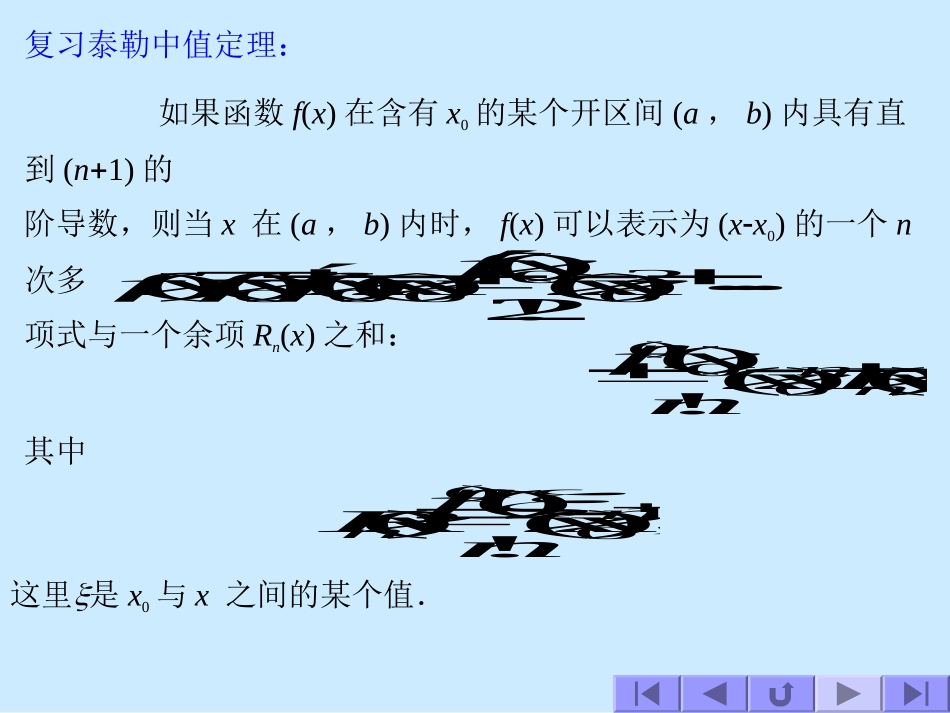
§11．4函数展开成幂级数一、泰勒级数二、函数展开成幂级数泰勒级数、函数展开成幂级数的步骤定理、麦克劳林级数展开式的唯一性函数ex的幂级数展开函数sinx的幂级数展开求幂级数展开式的间接展开法幂级数展开式小结一、泰勒级数本节讨论的问题是：给定函数f(x)，要考虑是否能找到这样一个幂级数，它在某区间内收敛，且其和恰好就是给定的函数f(x)．如果能找到这样的幂级数，我们就说，函数f(x)在该区间内能展开成幂级数．如果函数f(x)在含有x0的某个开区间(a，b)内具有直到(n1)的阶导数，则当x在(a，b)内时，f(x)可以表示为(xx0)的一个n次多项式与一个余项Rn(x)之和：这里是x0与x之间的某个值．复习泰勒中值定理：其中f(x)f(x0)f(x0)(xx0)!2)(0xf(xx0)2···!)(0)(nxfn(xx0)nRn(x)，Rn(x)!)()(nfn(xx0)n1，如果f(x)在点x0的某邻域内具有各阶导数f(x)，f(x)，···，f(n)(x)，···，则当n时，f(x)在点x0的泰勒多项式泰勒级数：成为幂级数这一幂级数称为函数f(x)的泰勒级数．显然，当xx0时，f(x)的泰勒级数收敛于f(x0)．pn(x)=f(x0)f(x0)(xx0)200)(!2)(xxxf···nnxxnxf)(!)(00)(f(x0)f(x0)(xx0)200)(!2)(xxxf···nnxxnxf)(!)(00)(···，需回答的问题：除了xx0外，f(x)的泰勒级数是否收敛?如果收敛，它是否一定收敛于f(x)?定理设函数f(x)在点x0的某一邻域U(x0)内具有各阶导数，则f(x)在该邻域内能展开成泰勒级数的充分必要条件是f(x)的泰勒公式中的余项Rn(x)当n时的极限为零，即nlimRn(x)0(xU(x0))．证明先证必要性．设f(x)在U(x0)内能展开为泰勒级数，即f(x)f(x0)f(x0)(xx0)200)(!2)(xxxf···nnxxnxf)(!)(00)(···．因为f(x)的n阶泰勒公式可写成f(x)sn1(x)Rn(x)，其中sn1(x)是f(x)的泰勒级数的前n1项的和，又在U(x0)内有sn1(x)f(x)(n)．于是Rn(x)f(x)sn1(x)0(n)．这就证明了条件是必要的．nlimRn(x)0(xU(x0))．证明再证充分性．设Rn(x)0(n)对一切xU(x0)成立．因为f(x)的n阶泰勒公式可写成f(x)sn1(x)Rn(x)，于是sn1(x)=f(x)Rn(x)f(x)(n)，即f(x)的泰勒级数在U(x0)内收敛，并且收敛于f(x)．定理设函数f(x)在点x0的某一邻域U(x0)内具有各阶导数，则f(x)在该邻域内能展开成泰勒级数的充分必要条件是f(x)的泰勒公式中的余项Rn(x)当n时的极限为零，即在泰勒级数麦克劳林级数：f(0)f(0)x2!2)0(xf···nnxnf!)0()(···，此级数称为f(x)的麦克劳林级数．f(x0)f(x0)(xx0)200)(!2)(xxxf···nnxxnxf)(!)(00)(···，中取x00，得事实上，如果f(x)在点x00的某邻域(R,R)内有幂级数展式f(x)a0a1xa2x2···anxn···，那么必有f(x)a12a2x3a3x2···nanxn1···，f(x)2!a23·2a3x···n·(n1)anxn2···，f(x)3!a3···n·(n1)(n2)anxn3···，···············f(n)(x)n!an(n1)n(n1)···2an1x···，···············把x=0代入以上各式，得a0f(0)，a1f(0)，a2!2)0(f，···，an!)0()(nfn，···．如果f(x)能展开成x的幂级数，那么这种展式是唯一的，它一定与f(x)的麦克劳林级数一致．展开式的唯一性：如果f(x)能展开成x的幂级数，那么这个幂级数就是f(x)的麦克劳林级数．但是，反过来如果f(x)的麦克劳林级数在点x00的某邻域内收敛，它却不一定收敛于f(x)．因此，如果f(x)在点x00处具有各阶导数，则f(x)的麦克劳林级数虽然能作出来，但这个级数是否在某个区间内收敛，以及是否收敛于f(x)却需要进一步考察．应注意的问题：二、函数展开成幂级数第一步求f(x)，f(x)，···，f(n)(x)，···．第二步求f(0)，f(0)，···，f(n)(0)，···．第三步写出幂级数函数展开成幂级数的步骤：f(0)f(0)x2!2)0(xf···nnxnf!)0()(···，并求出收敛半径R．第四步...