专题04几何压轴题-备战2022年中考数学满分真题模拟题分类汇编福建专用原卷版VIP免费

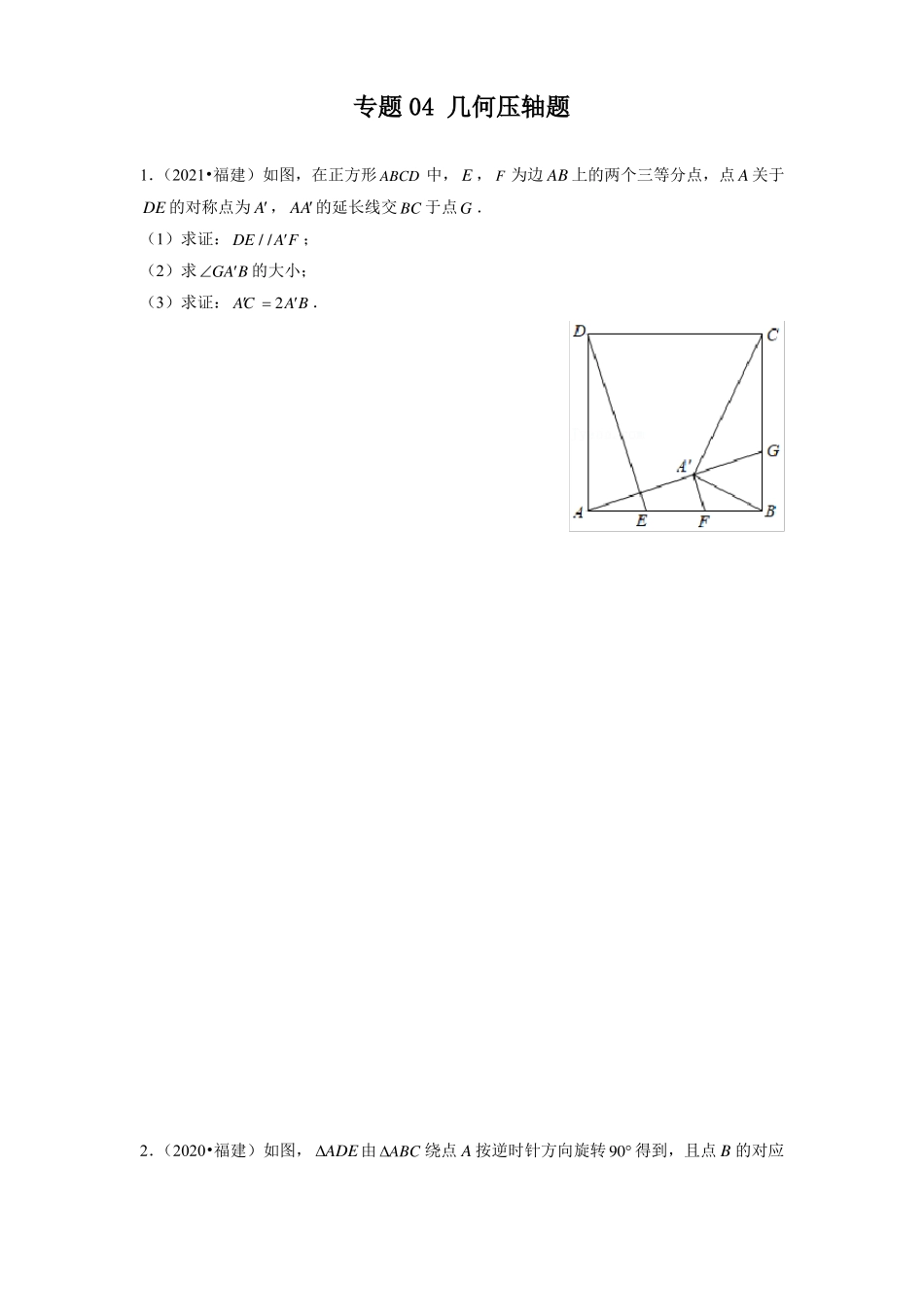
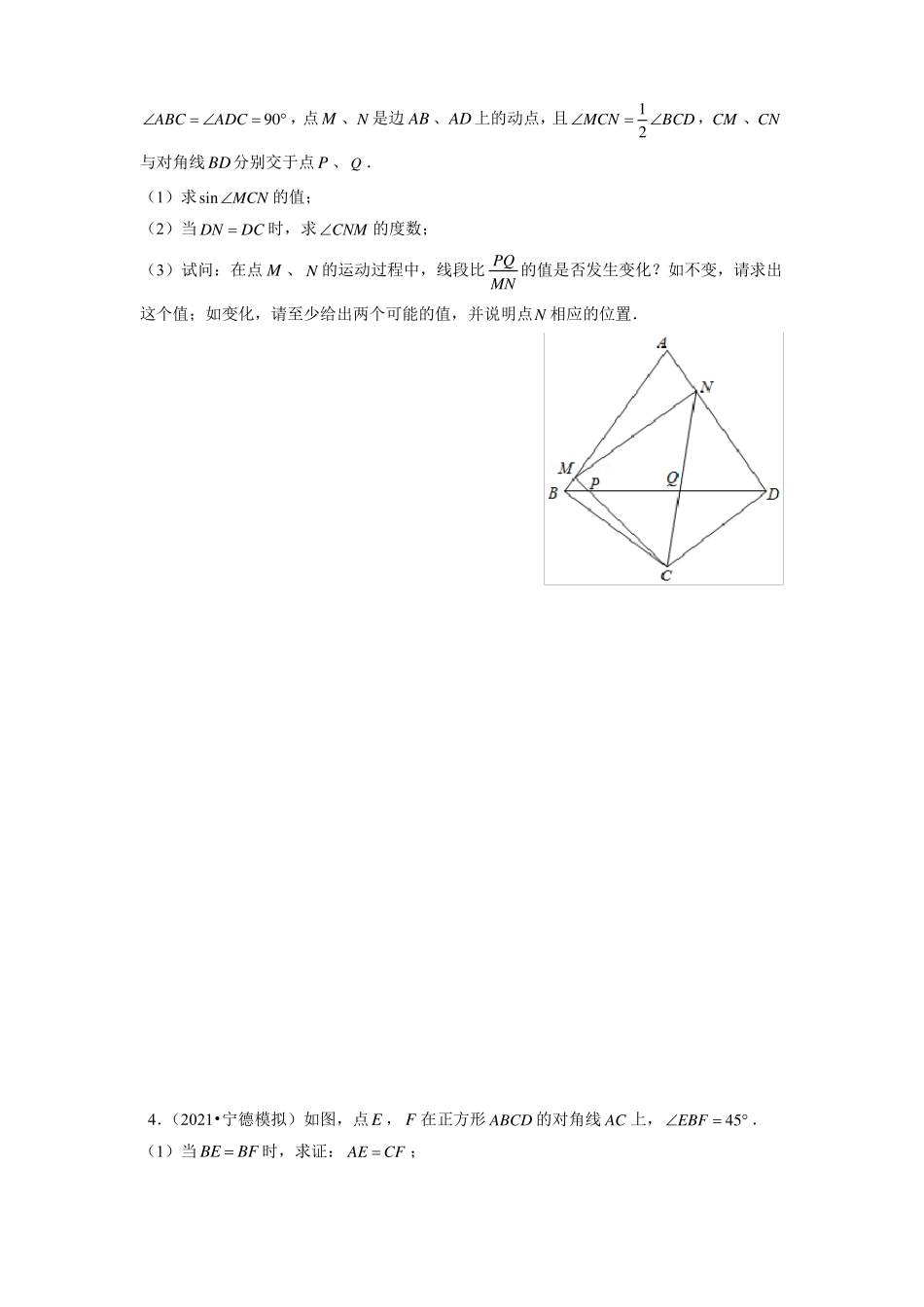
专题04几何压轴题1．（2021•福建）如图，在正方形ABCD中，E，F为边AB上的两个三等分点，点A关于DE的对称点为A，AA的延长线交BC于点G．（1）求证：DE//AF；（2）求GAB的大小；（3）求证：AC2AB．2．（2020•福建）如图，ADE由ABC绕点A按逆时针方向旋转90得到，且点B的对应点D恰好落在BC的延长线上，AD，EC相交于点P．（1）求BDE的度数；（2）F是EC延长线上的点，且CDFDAC．①判断DF和PF的数量关系，并证明；②求证：EPPCPFCF．3．（2021•泉州模拟）如图，边形ABCD中，ABAD4，CBCD3，四1点M、N是边AB、AD上的动点，且MCNBCD，CM、CNABCADC90，2与对角线BD分别交于点P、Q．（1）求sinMCN的值；（2）当DNDC时，求CNM的度数；（3）试问：在点M、N的运动过程中，线段比PQ的值是否发生变化？如不变，请求出MN这个值；如变化，请至少给出两个可能的值，并说明点N相应的位置．4．（2021•宁德模拟）如图，点E，F在正方形ABCD的对角线AC上，EBF45．（1）当BEBF时，求证：AECF；（2）若AB4，求AFCE的值；（3）延长BF交CD于点G，连接EG．判断线段BE与EG的数量关系，并说明理由．5．（2021•龙岩模拟）如图，RtABC中，ACB90，BC2，AC3，点D在RtABC的边AC上，DCm，以BD为直角边在AC同侧作等腰RtBDE，使BDDEn，过E作EFAC于点F，连接AE．（1）求证：EDFDBC；（2）求AE的最小值；5（3）若S四边形AEBCn，求S四边形AEBC的值．26．（2021•莆田模拟）如图1，矩形ABCD中，AB4，BC8，点E为BC边上的动点，连接DE．过点E作EFBD于点F，点G为DE的中点，连接CF，CG，GF．（1）求证：FGC2BDC；（2）设BEx，GFC的面积为S，①求S与x的函数关系式；②如图2，点M，N分别在AD，CD上，且DM取最小值时，求S的值．9，DN1，连接GM，GN，当GMGN27．（2021•三明模拟）在ABC和ADE中，ACBC，ADAE，ACBDAE90，点E在AB上，点F在EB上，BCFBDE．（1）如图①，若E是AB中点，CE延长线交BD于点G，求证：CEFBEG；（2）如图②，若E不是AB中点，①求证：CF1BD；2②求证：EFBF．8．（2021•泗水县一模）（1）如图1，正方形ABCD和正方形DEFG（其中ABDE)，连接CE，AG交于点H，请直接写出线段AG与CE的数量关系，位置关系；（2）如图2，矩形ABCD和矩形DEFG，AD2DG，AB2DE，ADDE，将矩形DEFG绕点D逆时针旋转(0360)，连接AG，CE交于点H，（1）中线段关系还成立吗？若成立，请写出理由；若不成立，请写出线段AG，CE的数量关系和位置关系，并说明理由；（3）矩形ABCD和矩形DEFG，AD2DG6，AB2DE8，将矩形DEFG绕点D逆时针旋转(0360)，直线AG，CE交于点H，当点E与点H重合时，请直接写出线段AE的长．9．（2021•漳州模拟）如图，在矩形ABCD中，AB2BC，点P、Q分别在AB、CD上，将矩形ABCD沿PQ折叠，使点B落在AD边上的点E处，点C落在点F处，EF交CD于点G，连接BE交PQ于点H．（1）求证：APEGQF；（2）求证：PQBH；（3）若sinGQF3，PQ310，求FG的长．510．（2021•南平模拟）如图，在矩形ABCD中，ABa，BCb，点E在CB的延长线上，点F在DE上，且EABFAB．（1）已知EBFB．①求AFD的度数；②当AEDDEC时，求a的值；b（2）求证：直线BF一定平分边AD．11．（2021•福建模拟）在ABC中，CACB，ACB．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当60时，是．BD的值是，直线BD与直线CP相交所成的较小角的度数CP（2）类比探究如图2，当90时，请写出就图2的情形说明理由．（3）解决问题当90时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，BD的值及直线BD与直线CP相交所成的较小角的度数，并CPP，D在同一直线上时AD的值．CP12．（2021•启东市模拟）定义：有一组对边相等且这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”．（1）如图①，四边形ABCD与四边形AEEG都是正方形...