TDS3000B数字荧光示波器观察波形的频率成分 (VIP免费

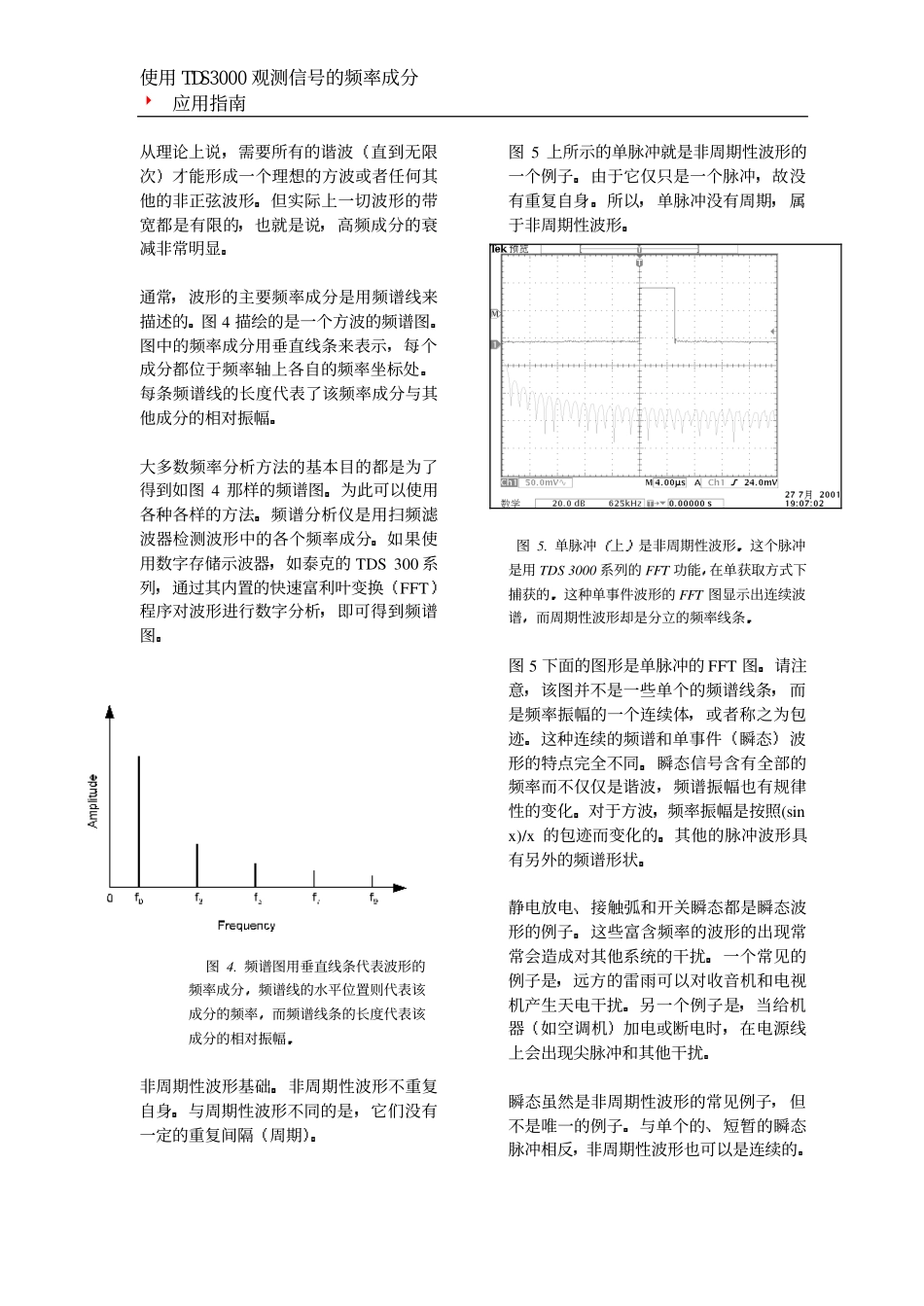
8应用指南检查波形的频率成分能够揭示出在普通的示波器图形中难以察觉的重要信息例如在标准的波形图上图1可能看不出波形的失真或对称性方面的问题但是只要看一下波形的频率成分图2那些问题就很明显了图1.图中的正弦波在普通的示波器画面上看来正常实际上却波形失真在图2所示的TDS300系列FFT画面上这种失真就很明显了图2.用TDS3000系列示波器显示在图1上看来正常的正弦波可以看出有失真存在失真的表现就在于除了正弦波的基波之外还出现了谐波图中的测量游标已设定在基波2兆赫兹上注意其三次谐波频率为6兆赫兹在过去观察波形的频率成分需要有频谱分析仪还要掌握仪器的使用技能现在对于深入的频率分析依然需要这样但是使用TDS3000系列数字荧光示波器观察波形的频率成分使用TDS3000观测信号的频率成分8应用指南很多基本的频率分析可以用泰克公司TDS3000这样的数字荧光示波器DPO来做图3.所有的周期性波形都是由一个基本正弦波和特定的谐波相加而成在本例中基波和三次五次七次和九次谐波相加以求得到一个方波为了更接近方波需要加入更高次的谐波为了能够观察波形的频率成分泰克TDS3000系列具有模块化的FFT傅立叶变换能力FFT实际上显示的是波形的频率成分这本应用笔记将介绍TDS3000系列FFT频率图的基本知识频率图的含义和使用方法波形的基本构成要了解FFT频率图就要首先了解波形及其基本构成波形又区分为周期性波形和非周期性波形为了简单起见我们先从周期性波形开始周期性波形基础周期性波形是按照一定的时间间隔或周期多次重复出现的波形正弦波方波和三角波都是常见的周期性波形按照傅立叶的理论所有的周期性波形都是由一组特定的正弦波组成的其中的基本正弦波也叫基波其频率与该波形的频率相同例如1千赫兹方波的基本正弦波的频率也是1千赫兹同样1千赫兹三角波的基本正弦波的频率也是1千赫兹从本质上说基波是波形中最重要的频率成分它决定了波形的频率或重复周期在所有的非正弦周期性波形中与基本成分同时存在的还有谐波谐波是频率为基波频率整倍数的正弦波例如1千赫兹方波的三次谐波是3千赫兹的正弦波而五次谐波为5千赫兹的正弦波依此类推直至无限除了具有特定的频率之外周期性波形的基波和谐波还具有特定的振幅和相位关系通过这些关系将基波和谐波叠加在一起就形成了特定的波形这一点在图3中有进一步的说明图中显示了一个方波的前五个频率成分相加在一起注意图3中合成的波形并不是一个准确的方波这是由于所加入的谐波还不够多若再加入更高次的谐波所得波形的过渡会更陡峭波角更直波顶和波底则更平坦使用TDS3000观测信号的频率成分8应用指南从理论上说需要所有的谐波直到无限次才能形成一个理想的方波或者任何其他的非正弦波形但实际上一切波形的带宽都是有限的也就是说高频成分的衰减非常明显通常波形的主要频率成分是用频谱线来描述的图4描绘的是一个方波的频谱图图中的频率成分用垂直线条来表示每个成分都位于频率轴上各自的频率坐标处每条频谱线的长度代表了该频率成分与其他成分的相对振幅大多数频率分析方法的基本目的都是为了得到如图4那样的频谱图为此可以使用各种各样的方法频谱分析仪是用扫频滤波器检测波形中的各个频率成分如果使用数字存储示波器如泰克的TDS300系列通过其内置的快速富利叶变换FFT程序对波形进行数字分析即可得到频谱图图4.频谱图用垂直线条代表波形的频率成分频谱线的水平位置则代表该成分的频率而频谱线条的长度代表该成分的相对振幅非周期性波形基础非周期性波形不重复自身与周期性波形不同的是它们没有一定的重复间隔周期图5上所示的单脉冲就是非周期性波形的一个例子由于它仅只是一个脉冲故没有重复自身所以单脉冲没有周期属于非周期性波形图5.单脉冲上是非周期性波形这个脉冲是用TDS3000系列的FFT功能在单获取方式下捕获的这种单事件波形的FFT图显示出连续波谱而周期性波形却是分立的频率线条图5下面的图形是单脉冲的FFT图请注意该图并不是一些单个的频谱线条而是频率振幅的一个连续体或者称之为包迹这种连续的频谱和单事件瞬态波形的特点完全不同瞬态信号含有全部的频率而不仅仅是谐波频谱振幅也有规律性的变化对于方波频率振幅是按照(sinx)/x的包迹...