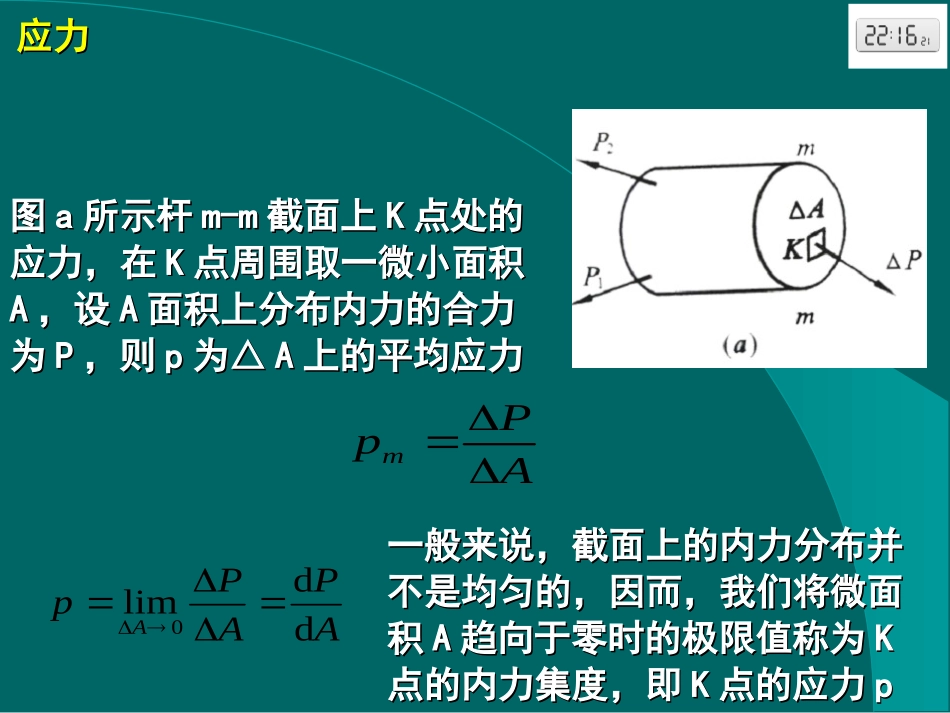
强度和变形计算一、应力二、轴向拉压杆件的变形、应变、胡克定律三、金属材料的拉伸、压缩的力学性质四、轴向拉压杆件的强度问题五、剪切、挤压问题的实用计算六、圆轴扭转强度计算七、弯曲应力一、应力一、应力概念概念杆件截面上某一点处的内力杆件截面上某一点处的内力集度称为该点的应力集度称为该点的应力应力应力APpm图图aa所示杆所示杆m-mm-m截面上截面上KK点处的点处的应力,在应力,在KK点周围取一微小面积点周围取一微小面积AA,设,设AA面积上分布内力的合力面积上分布内力的合力为为PP,则,则pp为△为△AA上的平均应力上的平均应力一般来说,截面上的内力分布并一般来说,截面上的内力分布并不是均匀的,因而,我们将微面不是均匀的,因而,我们将微面积积AA趋向于零时的极限值称为趋向于零时的极限值称为KK点的内力集度,即点的内力集度,即KK点的应力点的应力ppAPAPpAddlim0应力应力pp是一个矢量。通常情况下,它既不与截面垂直,是一个矢量。通常情况下,它既不与截面垂直,也不与截面相切。为了研究问题时方便,习惯上常将也不与截面相切。为了研究问题时方便,习惯上常将它分解为与截面垂直的分量它分解为与截面垂直的分量σσ和与截面相切的分量和与截面相切的分量ττ。。σσ称为正应力,称为正应力,ττ称为切应力。对于正应力称为切应力。对于正应力σσ规定:拉应力(箭头背离截面)为正,压应力(箭规定:拉应力(箭头背离截面)为正,压应力(箭头指向截面)为负;对于切应力头指向截面)为负;对于切应力ττ规定:顺时针规定:顺时针(切应力对研究部分内任一点取矩时,力矩的转向为(切应力对研究部分内任一点取矩时,力矩的转向为顺时针)为正,逆时针为负。顺时针)为正,逆时针为负。应力应力二、轴向拉压杆件的变形二、轴向拉压杆件的变形应变应变胡克定律胡克定律轴向拉压杆件的变形、应变、胡克定律轴向拉压杆件的变形、应变、胡克定律轴向拉(压)杆横截面上的正应力轴向拉(压)杆横截面上的内力是轴力,方向与横截面垂直。由内力与应力的关系,我们知道:在轴向拉(压)杆横截面上与轴力相应的应力只能是垂直于截面的正应力。而要确定正应力,必须了解内力在横截面上的分布规律,不能由主观推断。应力与变形有关,要研究应力,可以先从较直观的杆件变形入手。轴向拉压杆件的变形、应变、胡克定律轴向拉压杆件的变形、应变、胡克定律可以看到所有的纵向线都仍为直线,都伸长相等的长度;所有的横向线也仍为直线,保持与纵向线垂直,只是它们之间的相对距离增大了。由此,可以作出平面假设:变形前为平面的横截面,变形后仍为平面,但沿轴线发生了平移。由材料的均匀连续性假设可知,横截面上的内力是均匀分布的,即各点的应力相等轴向拉(压)杆横截面上只有一种应力轴向拉(压)杆横截面上只有一种应力————正应正应力,并且正应力在横截面上是均匀分布的,所以力,并且正应力在横截面上是均匀分布的,所以横截面上的平均应力就是任一点的应力。即拉横截面上的平均应力就是任一点的应力。即拉(压)杆横截面上正应力的计算公式为(压)杆横截面上正应力的计算公式为AFN对于等截面直对于等截面直杆,最大正应杆,最大正应力一定发生在力一定发生在轴力最大的截轴力最大的截面上。面上。AFNmaxmax轴向拉压杆件的变形、应变、胡克定律轴向拉压杆件的变形、应变、胡克定律轴向拉(压)杆斜截面上的应力2sin2sincossinpp2coscosp轴向拉压杆件的变形、应变、胡克定律轴向拉压杆件的变形、应变、胡克定律应力集中杆件截面尺寸的突然变化而引起局部应杆件截面尺寸的突然变化而引起局部应力急剧增大的现象,称为应力集中。力急剧增大的现象,称为应力集中。应力集中对杆件是不利的,实验表明:截面尺寸改变的越急剧,应力集中的现象越明显。因此,在设计时应尽可能不使杆的截面尺寸发生突变,避免带尖角的孔和槽,在阶梯轴和凸肩处要用圆弧过渡,并且要尽量使圆弧半径大一些。另外,应力集中对杆件强度的影响还与材料有关。轴向拉压杆件的变形、应变、胡克定律轴向拉压杆件的...