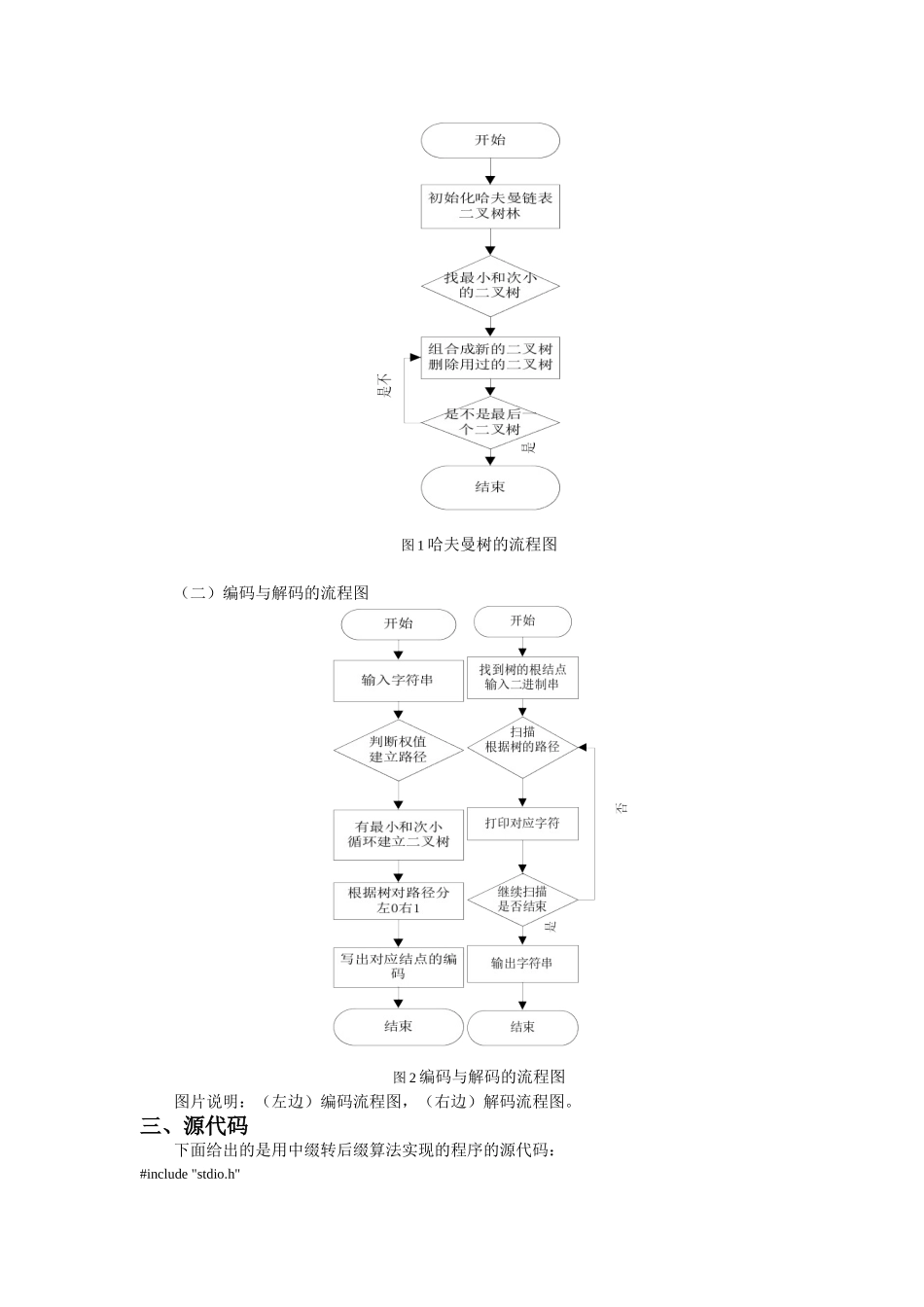
一、设计思想(一)哈夫曼树的设计思想对于一组具有确定权值的叶子结点可以构造出多个具有不同带权路径长度的二叉树,其中具有最小带权路径长度的二叉树称作哈夫曼树或最优二叉树。首先给定n个权值制造n个只含根结点的二叉树,得到一个二叉树林;再在这二叉树林里面找根结点的权值最小和次小的两棵树作成新的二叉树,其中新的二叉树的根结点的权值为左右子根结点权值之和;最后在二叉树林中把组合过的二叉树删除,再重复第二步直到最后就剩一颗二叉树的时候得到的这棵二叉树就是哈夫曼树。(二)哈夫曼编码与解码的设计思想在数据通讯中,经常要将传送的文字转换为二进制字符0和1组成的二进制串,称这个过程为编码。与子相对的是解码或是译码,就是用与编码相同的方式将二进制串转换称编码前的文字的过程称作解码。在这里是通过哈夫曼树实现编码与解码的,所以称作是哈夫曼编码与解码。首先输入一个字符串,还有相应的在哈夫曼树里的权值,这样用哈夫曼树把字符串用二进制串代替它,这个过程要注意树和编码问题,其中树的问题在上面已经解决,主要看编码的问题,就是根据我们输入的字符串和权值建立相应的树模型,这一步完成那编码就已经完成了,最后打印就行了;然后就是解码,完成编码相应的解码就相对简单了,就是先找到在编码的时候建的那个模型树,将编码中的二进制串再根据权值转换为相应的字符串,这样一步步解码就行了。以上就是通过用哈夫曼树进行哈夫曼编码与解码如何实现的主要设计思想。二、算法流程图(一)哈夫曼树的流程图图1哈夫曼树的流程图(二)编码与解码的流程图图2编码与解码的流程图图片说明:(左边)编码流程图,(右边)解码流程图。三、源代码下面给出的是用中缀转后缀算法实现的程序的源代码:#include"stdio.h"#include"string.h"#defineMAX100/*定义常量*/structHaffNode{intweight;/*权值*/intparent;/*双亲结点下标*/charch;intlchild;intrchild;}*myHaffTree;/*构造哈夫曼树*/structCoding{charbit[MAX];/*定义数组*/charch;intweight;/*字符的权值*/}*myHaffCode;/*定义结构体*/voidHaffman(intn)/*定义哈夫曼函数*/{inti,j,x1,x2,s1,s2;for(i=n+1;i<=2*n-1;i++)/*树的初始化*/{s1=s2=10000;x1=x2=0;for(j=1;j<=i-1;j++)/*构造哈夫曼树的非叶子结点*/{if(myHaffTree[j].parent==0&&myHaffTree[j].weight