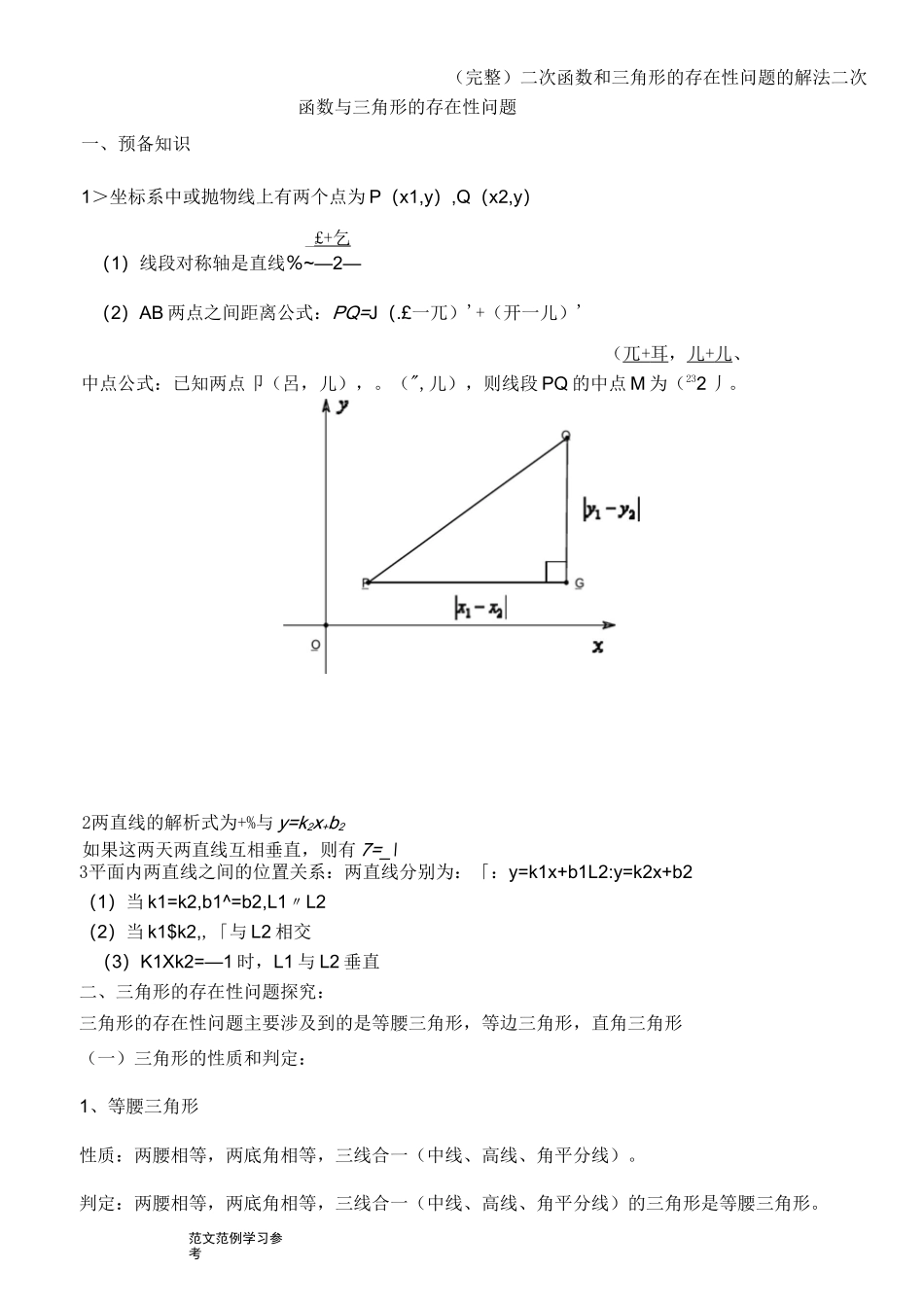
范文范例学习参考(完整)二次函数和三角形的存在性问题的解法二次函数与三角形的存在性问题一、预备知识1>坐标系中或抛物线上有两个点为P(x1,y),Q(x2,y)_£+乞(1)线段对称轴是直线%~—2—(2)AB两点之间距离公式:PQ=J(.£一兀)'+(开一儿)'(兀+耳,儿+儿、中点公式:已知两点卩(呂,儿),。(",儿),则线段PQ的中点M为(232丿。2两直线的解析式为+%与y=k2x+b2如果这两天两直线互相垂直,则有7=_\3平面内两直线之间的位置关系:两直线分别为:「:y=k1x+b1L2:y=k2x+b2(1)当k1=k2,b1^=b2,L1〃L2(2)当k1$k2,,「与L2相交(3)K1Xk2=—1时,L1与L2垂直二、三角形的存在性问题探究:三角形的存在性问题主要涉及到的是等腰三角形,等边三角形,直角三角形(一)三角形的性质和判定:1、等腰三角形性质:两腰相等,两底角相等,三线合一(中线、高线、角平分线)。判定:两腰相等,两底角相等,三线合一(中线、高线、角平分线)的三角形是等腰三角形。(完整)二次函数和三角形的存在性问题的解法范文范例学习参考范文范例学习参考如:已知两点A、B,在抛物线上求一点C,使得三角形ABC为等腰三角形解法:这是求点法:先运用两点间的距离公式分别求出线段ABBCAC的长度,第二步,作假设,(1)以点A为顶点的两条腰相等,即AB二AC(2)以点B为顶点的两条腰相等,即BA二BC(完整)二次函数和三角形的存在性问题的解法范文范例学习参考范文范例学习参考解:(1)将A(―1,0)、B(3,0)、C(0,3)代入抛物线y二ax'+bx+c中,得到抛物线的解析式:y=—x'+2x+3.(完整)二次函数和三角形的存在性问题的解法范文范例学习参考例1、如图:A(0,1)B(4,3)是直线y=1/2x+1±的两点,点p是x轴上一点,若AABP(完整)二次函数和三角形的存在性问题的解法范文范例学习参考(完整)二次函数和三角形的存在性问题的解法范文范例学习参考解得OP=I0J4OP=3,a.•.召1,0),目(3,0),2例2、(攀枝花)如图,抛物线y=ax2+bx+c经过点A(-3,0),B(1,0),C(0,-3).(1)求抛物线的解析式;(2)若点P为第三象限內抛物线上的一点,设APAC的面积为S,求S的最大值并求出此时点P的坐标;(3)设抛物线的顶点为D,DE丄x轴于点E,在y轴上是否存在点M,使得AADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.解:(1)由于抛物线y=ax2+bx+c经过A(—3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x~1),将C点坐标(0,—3)代入,得:a(0+3)(0一1)=-3,解得a=1,则y二(x+3)(X—1)=x2+2x—3,所以抛物线的解析式为:y二x'+2x—3;(2)过点P作x轴的垂线,交AC于点N.设直线AC的解析式为y二kx+m,由题意,得直线AC的解析式为:y=—x-3.设P点坐标为(x,x2+2x—3),则点N的坐标为(x,—x-3),/.PN=(-x—3)-(X2+2X-3)=—x2—3x.S=ipN-0A=丄x3|'-x:-3x'|=--;X4--^―VSAPAC=SAPAN+SAPCN,222>8・••当x=-2/3时,S有最大值27/8,此时点P的坐标为(-3/2,-15/4);(3)在y轴上是存在点M,能够使得AADM是直角三角形.理由如下:Vy=x2+2x-3=y=(x+1)2—4,.・.顶点D的坐标为(-1,一4),TA(-3,0),AD2=(-1+3)2+(-4—0)2=20.y*.OA即4_"=(完整)二次函数和三角形的存在性问题的解法设点M的坐标为(0,t),分三种情况进行讨论:(1)A为直角顶点时,如图3①,由勾股定理,解得t二3/2,所以点M的坐标为(0,3/2);②当D为直角顶点时,如图3②,由勾股定理,得DM2+AD2=AM2,即(0+1)3代+4)2+20二(0+3)2+(t—0)2,解得t二-7/2,所以点M的坐标为(0,—7/2);③当M为直角顶点时,如图3③,由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t—0)2+(0+1)2+(t+4)=20,解得t二一1或-3,所以点M的坐标为(0,—1)或(0,—3):综上可知,在y轴上存在点M,能够使得AADM是直角三角形,此时点M的坐标为(0,3/2)或(0,-7/2)或(0,-1)或(0,-3)・例3、如图,抛物线y=与x轴交于A、B两点,与y轴交于点C(0,-3).在抛物线上求点Q,使ABCQ是以BC为直角边的直角三角形.(完整)二次函数和三角形的存在性问题的解法范文范例学习参考(完整)二次函数和三角形的存在性问题的解法范文范例学习参考(完整)二次函数和三角形的存在性问题的解法范文范例学习参考(完整)二次函数和三角形的存在性问题的解法范文范例学习参考