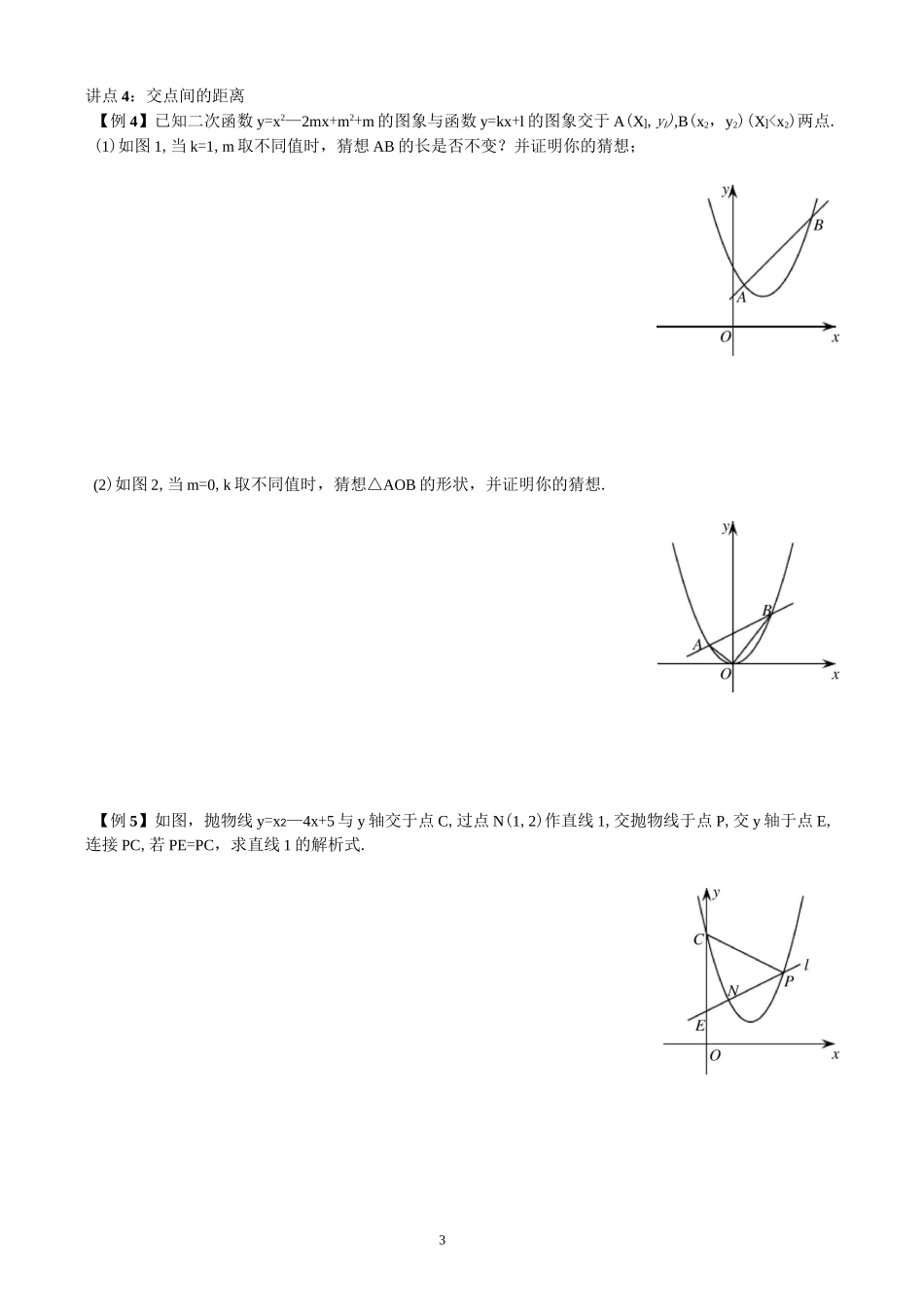
1二次函数与根的判别式、韦达定理讲点:公共点问题【例1】如图,抛物线y=—x2+4x—3的顶点为M,直线y=—2x—9与y轴交于点C,与直线MO交于点D,现将抛物线的顶点在直线OD上平移,平移后的抛物线与射线CD(含顶点C)只有一个公共点,求它的顶点横坐标的值或取值范围.【练】如图,已知抛物线y=—x2+2x+8与x轴交于点A,B两点,与y轴交于点C,点D为抛物线的顶点,直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?讲点2:距离问题【例2】如图,抛物线y=a(x—1)2+4与x轴交于A,B两点,与y轴交于点C,点D是抛物线的顶点,已知CD^2,在抛物线上共有三个点到直线BC的距离为m,求m的值.2【练】如图,抛物线y=ax2—6ax+5a与x轴交于A,B两点(A左,B右),若抛物线与直线y=2x的最近2斥点之间的距离为干,求a的值.讲点3:隐臧判别式【例3】如图,点P是直线l:y=—2x—2上的点,过点P的另一条直线m交抛物线y=x2与A,B两点,试证明:对于直线1上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.【练】如图,已知二次函数y=a(x2—6x+8)(a>0)的图象与x轴分别交于点A,B,与y轴交于点C,点D是抛物线的顶点.当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是否存在一个正数a,使得四条线段PA,PB,PC,PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)?请说明理由.3讲点4:交点间的距离【例4】已知二次函数y=x2—2mx+m2+m的图象与函数y=kx+l的图象交于A(X],yl),B(x2,y2)(X]0)与抛物线C交于A,B求U的值.5.如图1,抛物线C]:y=x2+4x+3顶点为M,抛物线C2与抛物线C]开口方向相反,形状相同,顶点为N,且M,N关于点P(0,2)对称.(1)求抛物线c2的解析式;(2)直线y=m交抛物线C]于点A,B,交抛物线C2于点C,D,若AB=2CD,求m的值;