第11章 结构稳定计算VIP免费

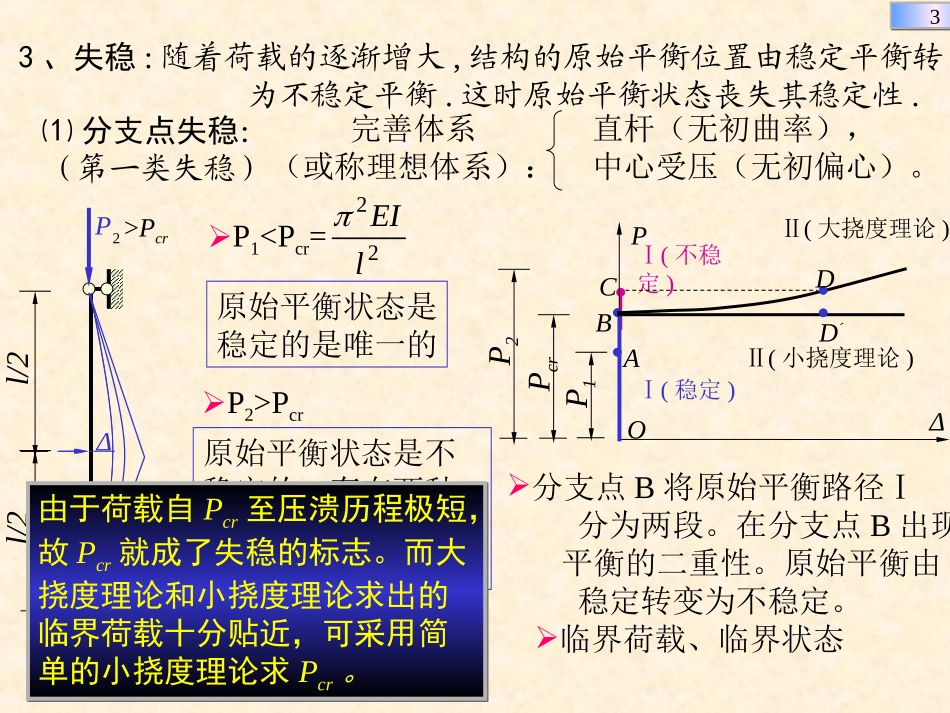
两类稳定问题概述稳定问题的分析方法弹性压杆稳定分析之静力法弹性压杆稳定分析之能量法刚架的稳定分析的有限单元法刚架的稳定分析的有限单元法两类稳定问题概述稳定问题的分析方法弹性压杆稳定分析之静力法弹性压杆稳定分析之能量法刚架的稳定分析的有限单元法刚架的稳定分析的有限单元法2211、、稳定验算的重要性设计结构强度演算刚度演算最基本的必不可少稳定性演算：2、平衡状态的三种情况稳定平衡：在某个平衡状态，轻微干扰，偏离原位，干扰消失，恢复原位。不稳定平衡：在某个平衡状态，轻微干扰，偏离原位，干扰消失，不能恢复原位，继续偏移。中性平衡：由稳定平衡到不稳定平衡的中间状态。§16-1两类稳定问题概述•高强度材料应用、结构形式的发展，结构趋于轻型、薄壁化，更易失稳，稳定计算日益重要。•失稳造成的工程事故时有发生。•1922华盛顿镍克尔卜克尔剧院倒塌；•1983社科院科研楼施工过程中，脚手架整体稳定性破坏……稳定是指：假设对结构施加一微小干扰使偏离其原位置，当干扰去除后，结构能恢复到原来的平衡位置稳定是指：假设对结构施加一微小干扰使偏离其原位置，当干扰去除后，结构能恢复到原来的平衡位置33C3、失稳:随着荷载的逐渐增大,结构的原始平衡位置由稳定平衡转为不稳定平衡.这时原始平衡状态丧失其稳定性.⑴分支点失稳：（第一类失稳）完善体系（或称理想体系）：直杆（无初曲率），中心受压（无初偏心）。Pl/2l/2PΔOP1PcrΔⅠ(稳定)Ⅰ(不稳定)Ⅱ(大挠度理论)Ⅱ(小挠度理论)DD´P2原始平衡状态是不稳定的。存在两种不同形式的平衡状态(直线、弯曲）。分支点B将原始平衡路径Ⅰ分为两段。在分支点B出现平衡的二重性。原始平衡由稳定转变为不稳定。临界荷载、临界状态2>Pcr由于荷载自Pcr至压溃历程极短，故Pcr就成了失稳的标志。而大挠度理论和小挠度理论求出的临界荷载十分贴近，可采用简单的小挠度理论求Pcr。由于荷载自Pcr至压溃历程极短，故Pcr就成了失稳的标志。而大挠度理论和小挠度理论求出的临界荷载十分贴近，可采用简单的小挠度理论求Pcr。44PcrPcrqcr原始平衡：轴向受压新平衡形式：压弯组合Pcr原始平衡：轴向受压新平衡形式：压弯组合原始平衡：平面弯曲新平衡形式：斜弯曲加扭转结构的变形产生了质的改变。即原来的平衡形式成为不稳定而可能出现新的与原来平衡形式有质的区别的平衡形式，同时，这种现象带有突然性。结构的变形产生了质的改变。即原来的平衡形式成为不稳定而可能出现新的与原来平衡形式有质的区别的平衡形式，同时，这种现象带有突然性。分支点失稳的特点：其它结构的分支点失稳55⑵极值点失稳：（第二类失稳）非完善体系：具有初曲率的压杆承受偏心荷载的压杆PPPΔOPcr(大挠度理论)(小挠度理论)PePe接近于中心压杆的欧拉临界荷载稳定问题与强度问题的区别：•强度问题是在稳定平衡状态下：max当,小变形，进行线性分析（一阶分析）。P当,大变形，进行几何非线性分析（二阶分析）。P重点是求内力、应力•稳定问题重点是研究荷载与结构抵抗力之间的平衡；找出变形急剧增长的临界点及相应的临界荷载。在变形后的几何位置上建立平衡方程，属于几何非线性分析（二阶分析）。•非线性分析，叠加原理不再适用。极值点失稳的特点：结构一开始受压就处于压弯状态，失稳与稳定无明显的界限，只是当接近失稳时，荷载增加很小，而挠度迅速增加。P-Δ曲线具有极值点。由于结构的变形过大，结构将不能正常使用。极值点失稳的特点：结构一开始受压就处于压弯状态，失稳与稳定无明显的界限，只是当接近失稳时，荷载增加很小，而挠度迅速增加。P-Δ曲线具有极值点。由于结构的变形过大，结构将不能正常使用。66Plk1、单自由度完善体系的分支点失稳EI=∞1）按大挠度理论分析PθRA0)cos()sin(lRlPsinklR0)sin)(cos(lklPPθOAPcrBⅠ(稳定)Ⅰ(不稳定)Ⅱ(大挠度理论)不稳定平衡Ⅱ(小挠度理论)随遇平衡0:可能解cosklPklPcr分支点A处的临界平衡也是不稳定的。对于这种具有不稳定分支点的完...