导数的几何意义VIP免费

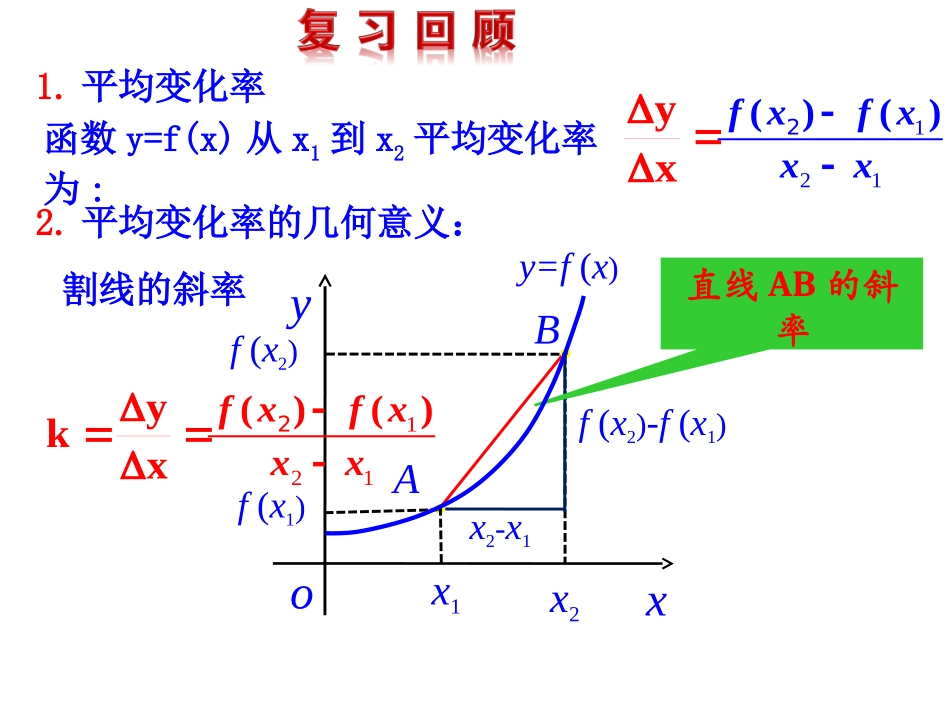
导数的几何意义l2l1AB0xyxyoBx2f(x2)Ax1f(x1)f(x2)-f(x1)x2-x1直线AB的斜率y=f(x)1.平均变化率函数y=f(x)从x1到x2平均变化率为:121()()2fxfxxxyx2.平均变化率的几何意义：割线的斜率121()()2fxfxxxykx3.导数的概念函数y=f(x)在x=x0处的瞬时变化率，反映了函数在x=x0附近的变化情况。0000(Δ)()()limxfxxfxfxx称为函数y=f(x)在x=x0处的导数,记作或,即0|xxy0()fx导数还可以用下式表示：0000()()()limxxfxfxfxxx4.求函数y=f(x)在x=x0处的导数的一般步骤是:001()()();yfxxfx求函数的增量002()()();求平均变化率fxxfxyxx003()()lim.取极限，得导数xyfxx一差、二比、三极限0()fx我们知道，导数表示函数y=f(x)在x=x0处的瞬时变化率，反映了函数f(x)在x=x0附近的变化情况。那么，导数的几何意义是什么呢？0()fxPl能否将圆的切线的概念推广为一般曲线的切线：直线与曲线有唯一公共点时，直线叫曲线过该点的切线？如果能，请说明理由；如果不能，请举出反例。不能xyo直线与圆相切时，只有一个交点P探究:如何定义一般曲线的切线？P1P2P3P4PTTTTPPxfyxfyxfyxfyOyxOyxOyxOyx211.图123400-,1,2,3,4,,?nnnnPxfxnfxPxfxPP观察如图1.12当点沿着曲线趋近于点时割线的变化趋势是什么PQoxyy=f(x)割线切线T结论:当Q点无限逼近P点时,此时直线PQ就是P点处的切线PT.点P处的割线与切线存在什么关系？xoyy=f(x)设曲线C是函数y=f(x)的图象，在曲线C上取一点P(x0,y0)及邻近一点Q(x0+x,y△0+y)△,过P,Q两点作割线，当点Q沿着曲线无限接近于点P点P处的切线。即△x→0时,如果割线PQ有一个极限位置PT,那么直线PT叫做曲线在曲线在某一点处的切线的定义△x△yPQTyxo)(xfyP相切相交如图直线l1是曲线C的切线吗?l2呢?l2l1AB0xyl1不是曲线C的切线，l2是曲线C的切线.PPnoxyy=f(x)割线切线T当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置，这个确定位置的直线PT称为点P处的切线.?同过的切线定义有什么不此处切线定义与以前学圆的切线定义并不适用于一般的曲线。通过逼近的方法，将割线趋于的确定位置的直线定义为切线（交点可能不惟一）适用于各种曲线。所以，这种定义才真正反映了切线的直观本质。2l1lxyABCxoyy=f(x)P(x0,y0)Q(x1,y1)M△x△y割线与切线的斜率有何关系呢？y()()xPQfxxfxkx＝即：当△x→0时，割线PQ的斜率的极限，就是曲线在点P处的切线的斜率，0000k()()limlimxxyxfxxfxx所以：P处的切线斜率＝当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即:xxfxxfxykxx)()(limlimtan0000切线这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限.要注意,曲线在某点处的切线:1)与该点的位置有关;2)要根据割线是否有极限来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.xoyy=f(x)PQ1Q2Q3Q4T213243PPQPQfxPQPQfxPQPQfxPPTPfxPfxPPT观察图像，可以发现，在点附近，比更贴紧曲线，比更贴紧曲线，比更贴紧曲线，过点的切线最贴紧点附近的曲线。因此，在点附近，曲线就可以用过点的切线近似代替。这是微积分中的重要思想方法－－以直代曲！继续观察图像的运动过程，还有什么发现？.,,..,.以直代曲想方法这是微积分中重要的思附近的曲线点这替近似代切线我们用曲线上某点处的这里近似代替无理数用有理数如例刻画复杂的对象数学上常用简单的对象14163函数y=f(x)在点x0处的导数的几何意义，就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率，即曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是.0()fx故曲线y=f(x)在点P(x0,f(x0))处的切线方程是:))(()(000xxxfxfy...