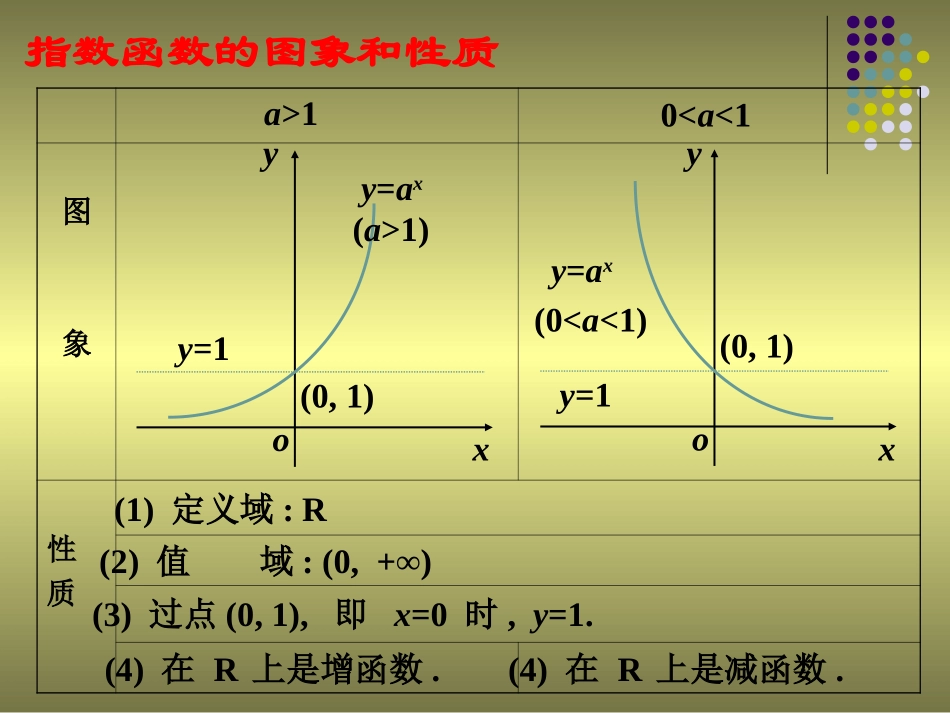
2.2.2对数函数及其性质(第一课时)复习引入1.指数与对数的互化关系),0,10(logRbNaaNbNaab且图象性质yox(0,1)y=1y=ax(a>1)a>1yox(0,1)y=1y=ax(0
100,a≠1)(5)非奇非偶函数(1)定义域:(0,+∞)(2)值域:R(4)在(0,+∞)上是减函数(4)在(0,+∞)上是增函数xyo(1,0)o(1,0)xy(3)过点(1,0),即x=1时,y=0例1求下列函数的定义域:2log)1(xya)4(log)2(xya(1)解:要使函数有意义,则:02x0x即:0xx故函数的定义域为三、对数函数性质应用(2)解:要使函数有意义,则:04x4x即得:4xx故函数的定义域为1、求下列函数的定义域:)1(log)1(5xy}1|{10-1)1(xxxx所以函数定义域为即因为解:xy311log)2(7}31|{3103-10311)2(xxxxx定义域即跟踪训练:例2:比较下列各组数中两个值的大小:(1);(2)8.5log3.4,log222.7log1.8,log0.30.3返回(1)因为函数y=log2x,它的底数2>1,所以在(0,+∞)上是增函数,又3.4<8.5,所以log23.4log0.32.7.分析:对数函数的增减性决定于对数的底数是大于1还是小于1,因此,要对底数a进行讨论解:当a>1时,函数在(0,+∞)上是增函数,于是loga5.1loga5.9.1)a0,(a5.9log5.1,log(3)aaxyalogxyalog2、比较下列各组数中两个值的大小:9log4,log(1)10105log3,log(2)0.50.50.5log0.4,log(3)3232ln7ln4,(4)9log4log1010解:5log3log0.50.50.5log0.4log3232ln7ln4跟踪训练:)1,0(log4,log(5)aaaaaaalog4log10)2(log4log1a(1)aa时,当时,当解:小结:对于底数是字母的,要分底大于1和在0-1之间讨论。变式训练:已知下列不等式,比较正数m、n的大小.)10(logloganmaa)1(logloganmaanm____nm____>>1函数y=logax,y=logbx,y=logcx的图象如下图所示,那么a,b,c的大小关系如何?答由图象可知a>1,b,c都大于0且小于1,由于y=logbx的图象在(0,1)上比y=logcx的图象靠近y轴,所以b100,a≠1)(5)非奇非偶函数(1)定义域:(0,+∞)(2)值域:R(4)在(0,+∞)上是减函数(4)在(0,+∞)上是增函数xyo(1,0)o(1,0)xy(3)过点(1,0),即x=1时,y=02、题型总结:(1)求对数函数的定义域。(2)比较同底的对数值的大小,当底数是相同的常数时,用函数的单调性比较;当底数是同一字母时,要对底数分类讨论。3、本节主要的思想方法:数形结合的思想类比的方法探究问题比较大小:5log,4log(2)7log,7log(1)6390.4课后作业:书74页第8题