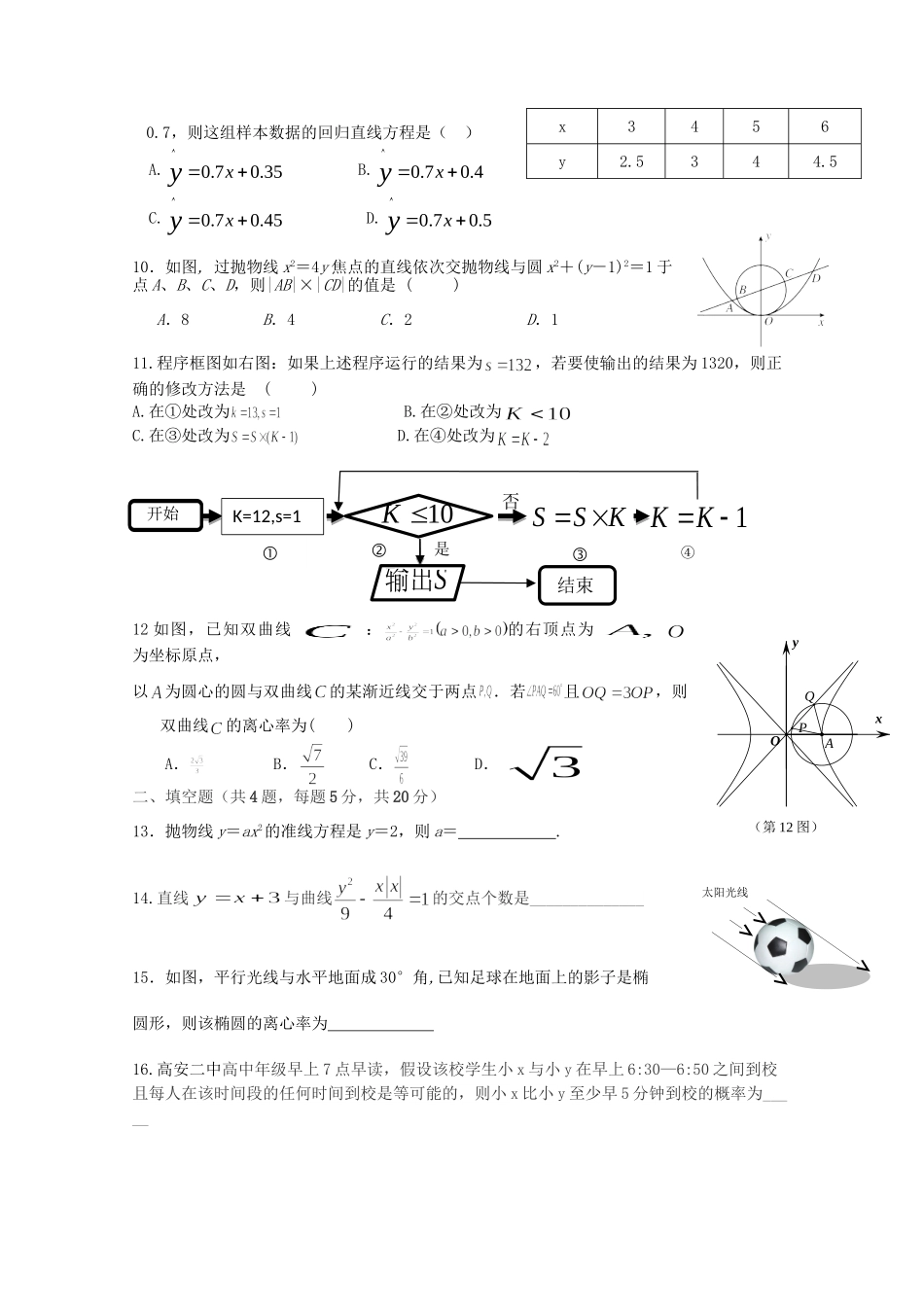
届樟树中学、高安二中期中考试高二数学(文)联考试题一、选择题(共12题,每题5分,共60分)1.“命题存在R,0”的否定是()A.不存在R,>0B.存在R,0C.对任意的R,0D.对任意的R,>02.椭圆的长轴为2,离心率为,则其短半轴为()A.B.C.D.3.0,0xy“,则221xy”“是1xy”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件4.已知数据是高安市个普通职工的年的年收入,设这个数据的中位数为,平均数为,方差为,如果再加上比尔.盖茨的年的年收入(约80亿美元),则这个数据中,下列说法正确的是()A.年收入平均数大大增大,中位数一定变大,方差可能不变B.年收入平均数大大增大,中位数可能不变,方差变大C.年收入平均数大大增大,中位数可能不变,方差也不变D.年收入平均数可能不变,中位数可能不变,方差可能不变。5.经过抛物线y2=4x的焦点且垂直于直线3x-2y=0的直线l的方程是()A.3x-2y-3=0B.6x-4y-3=0C.2x+3y-2=0D.2x+3y-1=06.一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是()A.B.C.D.7.中心均为原点O的双曲线与椭圆有公共焦点,M,N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是()A.3B.2C.D.8.如图是11月6日下午高安二中红歌会比赛中七位评委为某班级打出的分数的茎叶图,去掉一个最高分和一个最低分后所剩数据的平均分为85分,则的最小值为()A.6B.7C.8D.99.某工厂生产某种产品的产量x(吨)与相应的生产能耗y(吨标准煤)有如下几组样本数据:据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为yxAQPO(第12图)开始S输出10K是否K=12,s=11KKKSS④结束0.7,则这组样本数据的回归直线方程是()A.0.70.35xyB.0.70.4xyC.0.70.45xyD.0.70.5xy10.如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则|AB|×|CD|的值是()A.8B.4C.2D.111.程序框图如右图:如果上述程序运行的结果为,若要使输出的结果为1320,则正确的修改方法是()A.在①处改为B.在②处改为C.在③处改为D.在④处改为12如图,已知双曲线:的右顶点为为坐标原点,以为圆心的圆与双曲线的某渐近线交于两点.若且,则双曲线的离心率为()A.B.C.D.二、填空题(共4题,每题5分,共20分)13.抛物线y=ax2的准线方程是y=2,则a=.14.直线与曲线的交点个数是______________15.如图,平行光线与水平地面成30°角,已知足球在地面上的影子是椭圆形,则该椭圆的离心率为16.高安二中高中年级早上7点早读,假设该校学生小x与小y在早上6:30—6:50之间到校且每人在该时间段的任何时间到校是等可能的,则小x比小y至少早5分钟到校的概率为_____x3456y2.5344.5太阳光线三解答题(17题10分,18-22题每题12分,共70分)17.已知命题对,不等式恒成立;命题,使不等式成立;若是真命题,是假命题,求的取值范围.18.“世界睡眠日”定在每年的3月21日.年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图,(1)求表格中m与n的值(2)求输出S的值(3)S的统计意义是什么?19.已知关于x的二次函数f(x)=ax2﹣4bx+1.(1)设集合P={1,2,3}和Q={﹣1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;(2)设点(a,b)是区域内的一点,求y=f(x)在区间[1,+∞)上是增函数的概率.序号(i)分组睡眠时间组中值(mi)频数(人数)频率(fi)1[4,5)4.580.042[5,6)5.5520.263[6,7)6.5m0.304[7,8)7.5560.285[8,9)8.520n6[9,10]9.540.0220.在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,再将该小球...