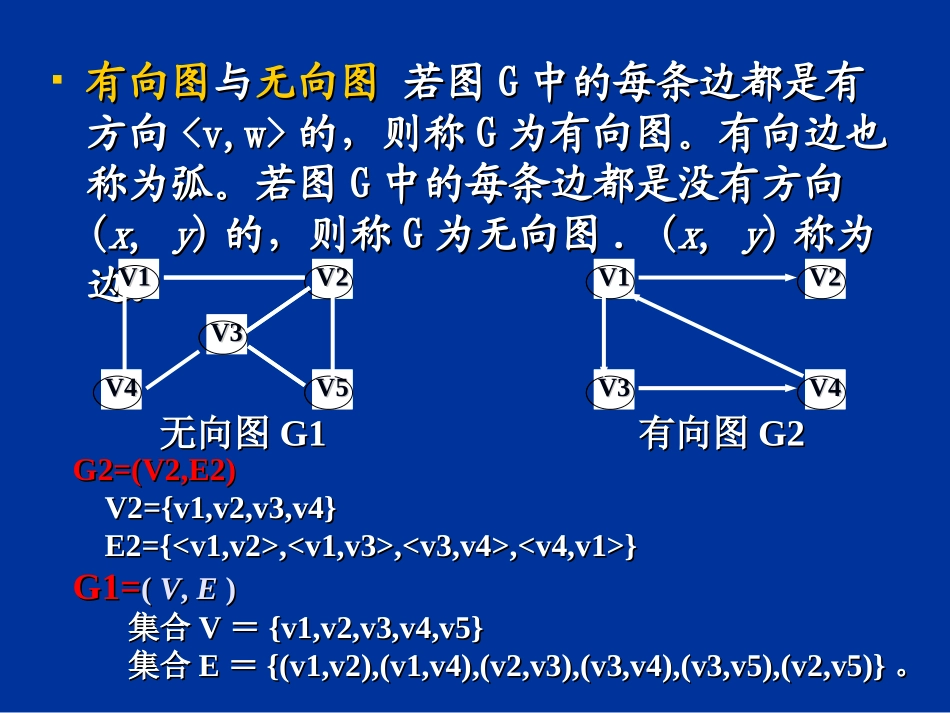
图的基本概念图的基本概念图的存储结构图的存储结构图的遍历图的遍历最小生成树最小生成树最短路径方法最短路径方法图的基本概念图的基本概念图定义图定义图是由顶点集合图是由顶点集合(vertex)(vertex)及顶点间的及顶点间的关系关系边(或者弧边(或者弧))集合组成的一种数据结构:集合组成的一种数据结构:GraphGraph==((VV,,EE))其中其中VV={={xx||xx某个数据对象某个数据对象}}是顶是顶点的有穷点的有穷非空集合;非空集合;EE={={或或(v,w)|(v,w)|vv,,wwVV}}是顶点之间关系的有穷集合,谓词是顶点之间关系的有穷集合,谓词P(v,w)P(v,w)定义了定义了弧弧的意义或信息的意义或信息,,谓词是用来刻划个体谓词是用来刻划个体词的性质或事物之间关系的词词的性质或事物之间关系的词..有向图有向图与与无向图无向图若图若图GG中的每条边都是有中的每条边都是有方向方向的,则称的,则称GG为有向图。有向边也为有向图。有向边也称为弧。若图称为弧。若图GG中的每条边都是没有方向中的每条边都是没有方向((xx,,yy))的,则称的,则称GG为无向图为无向图..((xx,,yy))称为称为边。边。V1V1V3V3V4V4V5V5V2V2V4V4V3V3V2V2V1V1无向图无向图G1G1有向图有向图G2G2G2=(V2,E2)G2=(V2,E2)V2={v1,v2,v3,v4}V2={v1,v2,v3,v4}E2={,,,}E2={,,,}G1=G1=((VV,,EE))集合集合VV=={v1,v2,v3,v4,v5}{v1,v2,v3,v4,v5}集合集合EE=={(v1,v2),(v1,v4),(v2,v3),(v3,v4),(v3,v5),(v2,v5)}{(v1,v2),(v1,v4),(v2,v3),(v3,v4),(v3,v5),(v2,v5)}。。V1V1V3V3V4V4V5V5V2V2V4V4V3V3V2V2V1V124/12/264权权某些图的边具有与它相关的数某些图的边具有与它相关的数,,称称之为权。在实际应用中,权值可以有某之为权。在实际应用中,权值可以有某种含义。比如,在一个反映城市交通线种含义。比如,在一个反映城市交通线路的图中,边上的权值可以表示该条线路的图中,边上的权值可以表示该条线路的长度或者等级;对于一个电子线路路的长度或者等级;对于一个电子线路图,边上的权值可以表示两个端点之间图,边上的权值可以表示两个端点之间的电阻、电流或电压值;对于反映工程的电阻、电流或电压值;对于反映工程进度的图而言,边上的权值可以表示从进度的图而言,边上的权值可以表示从前一个工程到后一个工程所需要的时间前一个工程到后一个工程所需要的时间等等。等等。带权图叫做网。有向网、无向网。带权图叫做网。有向网、无向网。12356874ABDCE107966712315166030453580407560804024/12/266完全图完全图对有对有nn个顶点的图,若为有向图个顶点的图,若为有向图且边数为且边数为n(n-1)n(n-1),则称其为,则称其为有向完全图有向完全图。。若为无向图且边数为若为无向图且边数为n(n-1)/2n(n-1)/2,则称其,则称其为为无向完全图无向完全图;边或弧数;边或弧数>,,称称vvii邻接到邻接到vvjj,,弧弧>关联于顶点关联于顶点vvii和和vvjj..顶点的度一个顶点顶点的度一个顶点vv的度是与它相关联的边的条的度是与它相关联的边的条数。记作数。记作TD(TD(vv))。。顶点顶点vv的入度的入度是以是以vv为终点的有向边的条数为终点的有向边的条数,,记作记作ID(ID(vv););顶点顶点vv的出度的出度是以是以vv为始点的有向边的条为始点的有向边的条数数,,记作记作OD(OD(vv))。。子图子图设有两个图设有两个图GG==((VV,,EE))和和G‘G‘==((VV’,’,EE‘)‘)。。若若VV’’VV且且EE‘‘EE,,则称图则称图G’G’是图是图GG的子图的子图。。511(()())2neI...