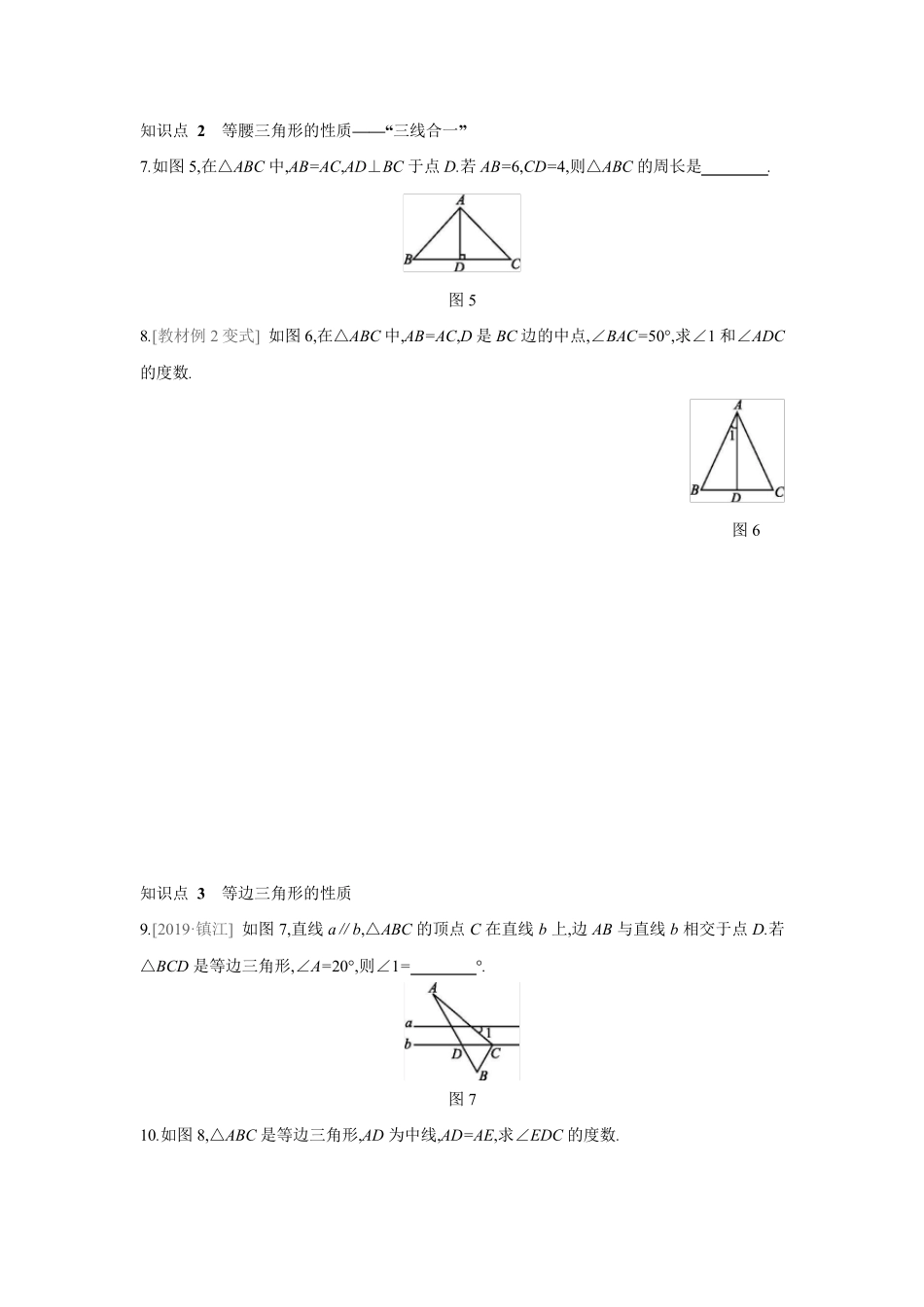
13.3.1等腰三角形的性质【基础练习】知识点1等腰三角形的性质定理1.如图1,在△ABC中,AB=AC,∠B=70°,则∠A的度数是()图1A.70°B.55°C.50°D.40°2.[2019·抚顺]若一个等腰三角形的两边长分别为2,4,则第三边的长为()A.2B.3C.4D.2或43.[2019·毕节]如图2,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连结AD.若∠B=40°,∠C=36°,则∠DAC的度数为°.图24.如图3,在△ABC中,AB=AC,BD⊥AC于点D,且∠DBC=25°,则∠A=°.图35.已知等腰三角形的一个外角为130°,则它的顶角的度数为.6.已知:如图4,在△ABC中,AB=AC,AE是外角∠CAD的平分线.求证:AE∥BC.图4知识点2等腰三角形的性质——“三线合一”7.如图5,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,CD=4,则△ABC的周长是.图58.[教材例2变式]如图6,在△ABC中,AB=AC,D是BC边的中点,∠BAC=50°,求∠1和∠ADC的度数.图6知识点3等边三角形的性质9.[2019·镇江]如图7,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1=°.图710.如图8,△ABC是等边三角形,AD为中线,AD=AE,求∠EDC的度数.图8【能力提升】11.[2019·宁夏]如图9,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE,连结DE,过点A的直线GH与DE平行.若∠C=40°,则∠GAD的度数为()图9A.40°B.45°C.55°D.70°12.如图10,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于()图10A.30°B.40°C.45°D.36°13.已知:如图11,在△ABC中,AB=AC,中线BE,CD相交于点O.求证:BE=CD.图1114.如图12,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°.(1)求∠DBC的度数;(2)求证:BD=CE.图1215.如图13所示,∠BAC=∠ABD,AC=BD,O是AD,BC的交点,E是AB的中点.试判断OE和AB的位置关系,并给出证明.图13【能力提升】16.如图14,在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.(1)当点D在BC的什么位置时,DE=DF?证明你的结论;(2)如图②,过点C作AB边上的高CG,试猜想DE,DF,CG的长之间存在怎样的数量关系(直接写出你的结论)?图14答案1.D2.C[解析]①当4是腰长时,三角形的三边长分别为4,4,2,能组成三角形,∴第三边长为4;②当4是底边长时,三角形的三边长分别为2,2,4,∵2+2=4,∴不能组成三角形.综上所述,第三边长为4.故选C.3.34[解析]∵∠B=40°,∠C=36°,∴∠BAC=180°-∠B-∠C=104°.∵AB=BD,∴∠BAD=∠ADB=(180°-∠B)÷2=70°,∴∠DAC=∠BAC-∠BAD=34°.故答案为34.4.50[解析]∵BD⊥AC,∴∠DBC+∠C=90°.∵∠DBC=25°,∴∠C=65°.∵AB=AC,∴∠ABC=∠C=65°,∴∠A=180°-(∠ABC+∠C)=180°-130°=50°.故答案为50.5.50°或80°6.证明:∵AE是∠CAD的平分线,∴∠CAD=2∠DAE.∵AB=AC,∴∠B=∠C.又∵∠CAD=∠B+∠C=2∠B,∴∠DAE=∠B,∴AE∥BC.7.20[解析]∵在△ABC中,AB=AC,∴△ABC是等腰三角形.又∵AD⊥BC于点D,∴BD=CD.∵AB=6,CD=4,∴△ABC的周长为6+4+4+6=20.故答案为20.8.解:∵在△ABC中,AB=AC,D是BC边的中点,∴AD平分∠BAC,AD⊥BC,∴∠1=12∠BAC=12×50°=25°,∠ADC=90°.9.40[解析]∵△BCD是等边三角形,∴∠BDC=60°.∵a∥b,∴∠2=∠BDC=60°.由三角形的外角性质可知,∠1=∠2-∠A=40°.故答案为40.10.解:∵△ABC是等边三角形,AD为中线,∴AD⊥BC,∠CAD=12∠BAC=30°,∴∠ADC=90°.∵AD=AE,∴∠ADE=∠AED=180°-∠ᵃᵃᵃ2=180°-30°2=75°,∴∠EDC=∠ADC-∠ADE=90°-75°=15°.11.C[解析]∵AC=CB,∠C=40°,∴∠BAC=∠B=12(180°-40°)=70°.∵AD=AE,∴∠ADE=∠AED=(180°-70°)÷2=55°.∵GH∥DE,∴∠GAD=∠ADE=55°.故选C.12.D[解析]设∠A=x.∵AD=BD,∴∠ABD=∠A=x,∴∠BDC=2x.∵BD=BC,∴∠C=∠BDC=2x.∵AB=AC,∴∠ABC=∠C=2x.在△ABC中,∵∠A+∠ABC+∠C=180°,即x+2x+2x=180°,∴x=36°,∴∠A=36°.故选D.13.证明:∵BE,CD是△ABC的中线,∴BD=12AB,CE=12AC.∵AB=AC,∴BD=CE,∠ABC=∠ACB.在△BCD和△CBE中,∵BD=CE,∠DBC=∠ECB,BC=CB,∴△BCD≌△CBE(S.A.S.),∴BE=CD.14.解:(1)∵△ABD是等腰直角三角形,∠BAD=90°,∴∠DBA=45°.∵AB=AC,∠BAC=40°,∴∠ABC=70°,∴∠DBC=∠DBA+∠ABC=115°.(2)证明:∵△ABD和△ACE均为等腰直角三角形,∠BAD=∠CAE=90°,∴AB=AD,AC=AE.又∵AB=AC,∴AB=AD=AC=AE,∴△ABD≌△ACE,∴BD=CE.15.解:OE⊥AB.证明:在△BAC和△ABD中,∵AC=BD,∠BAC=∠ABD,AB=BA,∴△BAC≌△ABD,∴∠OBA=∠OAB,∴∠OAC=∠OBD.又∵∠AOC=∠BOD,AC=BD,∴△AOC≌△BOD,∴OA=OB.又∵E是AB的中点,∴OE⊥AB.16.解:(1)当点D在BC的中点时,DE=DF.证明:∵D为BC的中点,∴BD=CD.∵AB=AC,∴∠B=∠C.∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°.在△BED和△CFD中,∵∠B=∠C,∠DEB=∠DFC,BD=CD,∴△BED≌△CFD(A.A.S.),∴DE=DF.(2)CG=DE+DF.证明:如图,连结AD.∵S△ABC=S△ADB+S△ADC,∴12AB·CG=12AB·DE+12AC·DF.∵AB=AC,∴CG=DE+DF.