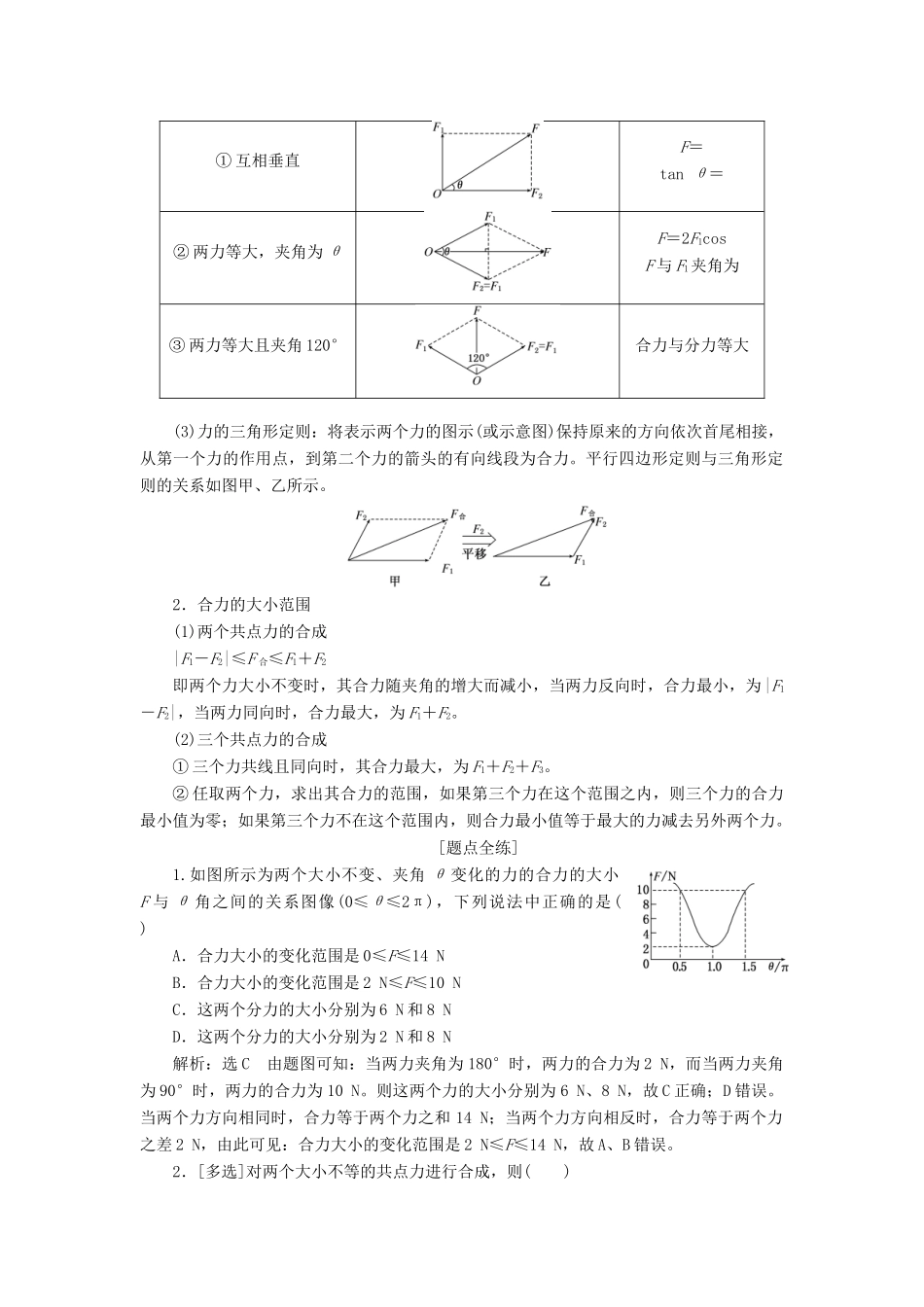
力的合成与分解(1)合力及其分力均为作用于同一物体上的力。(√)(2)合力及其分力可以同时作用在物体上。(×)(3)几个力的共同作用效果可以用一个力来代替。(√)(4)在进行力的合成与分解时,都要应用平行四边形定则或三角形定则。(√)(5)两个力的合力一定比其分力大。(×)(6)互成角度的两个力的合力与分力间一定构成封闭的三角形。(√)(7)既有大小又有方向的物理量一定是矢量。(×)突破点(一)力的合成问题1.共点力合成的常用方法(1)作图法:从力的作用点起,按同一标度作出两个分力F1和F2的图示,再以F1和F2的图示为邻边作平行四边形,画出过作用点的对角线,量出对角线的长度,计算出合力的大小,量出对角线与某一力的夹角确定合力的方向(如图所示)。(2)计算法:几种特殊情况的共点力的合成。类型作图合力的计算①互相垂直F=tanθ=②两力等大,夹角为θF=2F1cosF与F1夹角为③两力等大且夹角120°合力与分力等大(3)力的三角形定则:将表示两个力的图示(或示意图)保持原来的方向依次首尾相接,从第一个力的作用点,到第二个力的箭头的有向线段为合力。平行四边形定则与三角形定则的关系如图甲、乙所示。2.合力的大小范围(1)两个共点力的合成|F1-F2|≤F合≤F1+F2即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小,为|F1-F2|,当两力同向时,合力最大,为F1+F2。(2)三个共点力的合成①三个力共线且同向时,其合力最大,为F1+F2+F3。②任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力最小值为零;如果第三个力不在这个范围内,则合力最小值等于最大的力减去另外两个力。[题点全练]1.如图所示为两个大小不变、夹角θ变化的力的合力的大小F与θ角之间的关系图像(0≤θ≤2π),下列说法中正确的是()A.合力大小的变化范围是0≤F≤14NB.合力大小的变化范围是2N≤F≤10NC.这两个分力的大小分别为6N和8ND.这两个分力的大小分别为2N和8N解析:选C由题图可知:当两力夹角为180°时,两力的合力为2N,而当两力夹角为90°时,两力的合力为10N。则这两个力的大小分别为6N、8N,故C正确;D错误。当两个力方向相同时,合力等于两个力之和14N;当两个力方向相反时,合力等于两个力之差2N,由此可见:合力大小的变化范围是2N≤F≤14N,故A、B错误。2.[多选]对两个大小不等的共点力进行合成,则()A.合力一定大于每个分力B.合力可能同时垂直于两个分力C.合力的方向可能与一个分力的方向相反D.两个分力的夹角θ在0°到180°之间变化时,θ角越小,合力越大解析:选CD不在同一条直线上的两个力合成时,遵循平行四边形定则,故合力可能大于、小于或等于任意一个分力,A错误;合力是两分力构成的平行四边形的对角线,而对角线不可能同时垂直两个边,B错误;当两分力方向相反时,则合力可以与一个分力的方向相反,即与较小力的方向相反,C正确;两个大小不变的力,其合力随两力夹角的减小而增大,当夹角为零时,合力最大,D正确。3.一物体受到三个共面共点力F1、F2、F3的作用,三力的矢量关系如图所示(小方格边长相等),其中F3=4N。下列说法正确的是()A.三力的合力有最大值14.3N,方向不确定B.三力的合力有唯一值8N,方向与F3同向C.三力的合力有唯一值12N,方向与F3同向D.由题给条件无法求出合力大小解析:选C根据平行四边形定则,作出F1、F2的合力如图所示,大小等于2F3,方向与F3相同,再跟F3合成,两个力同向,则三个力的合力大小为3F3=12N,方向与F3同向,C正确。突破点(二)力的分解问题1.按作用效果分解力的一般思路2.正交分解法(1)定义:将已知力按互相垂直的两个方向进行分解的方法。(2)建立坐标轴的原则:一般选共点力的作用点为原点,在静力学中,以少分解力和容易分解力为原则(即尽量多的力在坐标轴上);在动力学中,通常以加速度方向和垂直加速度方向为坐标轴建立坐标系。(3)方法:物体受到F1、F2、F3、…多个力作用求合力F时,可把各力沿相互垂直的x轴、y轴分解。x轴上的合力:Fx=Fx1+Fx2+Fx3+…y轴上的合力:Fy=Fy1+Fy2+Fy3+…合力大小:F=合力方向:与x轴夹角设为θ,则tanθ=。[典例](2019·泰安模拟)用...