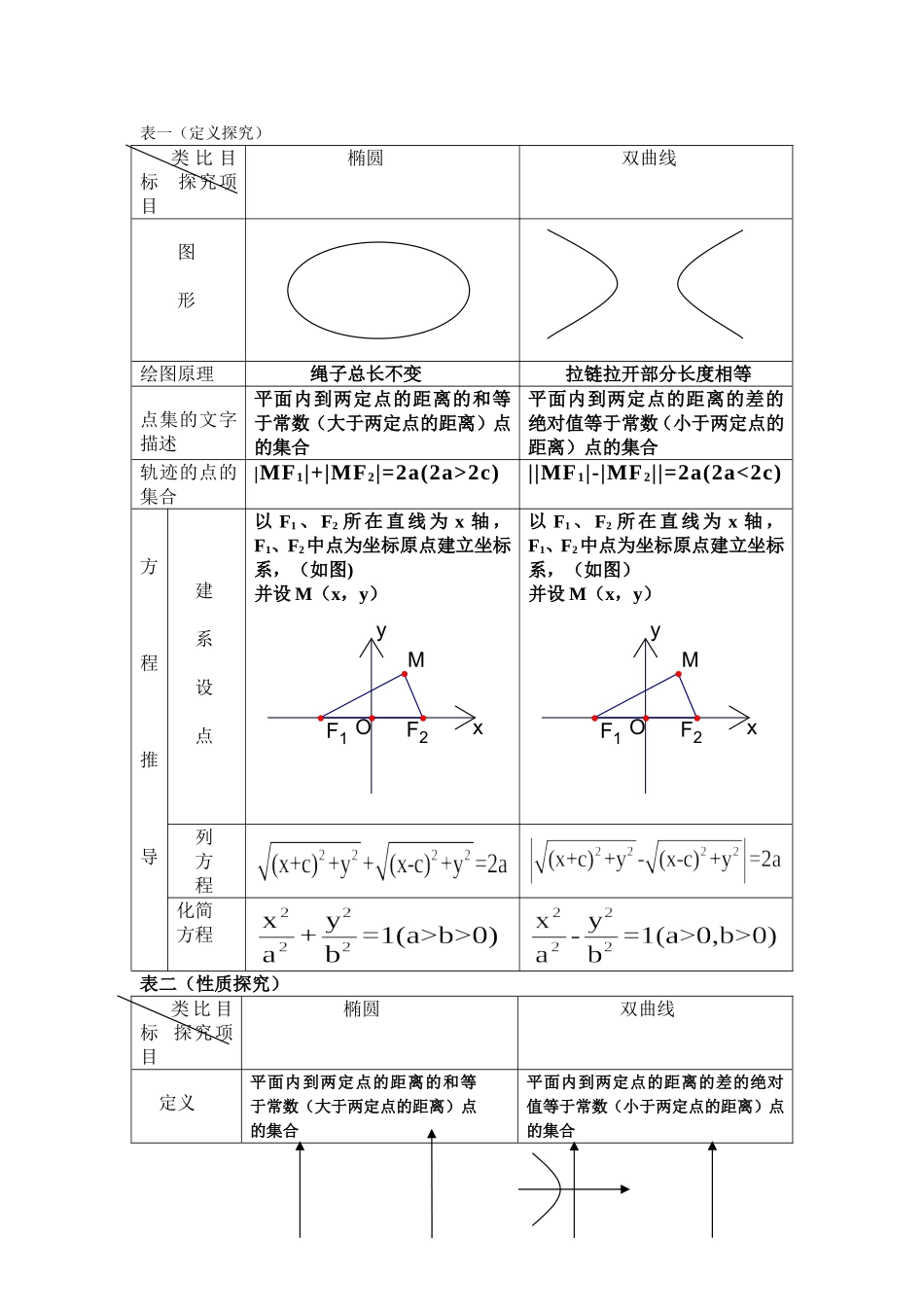
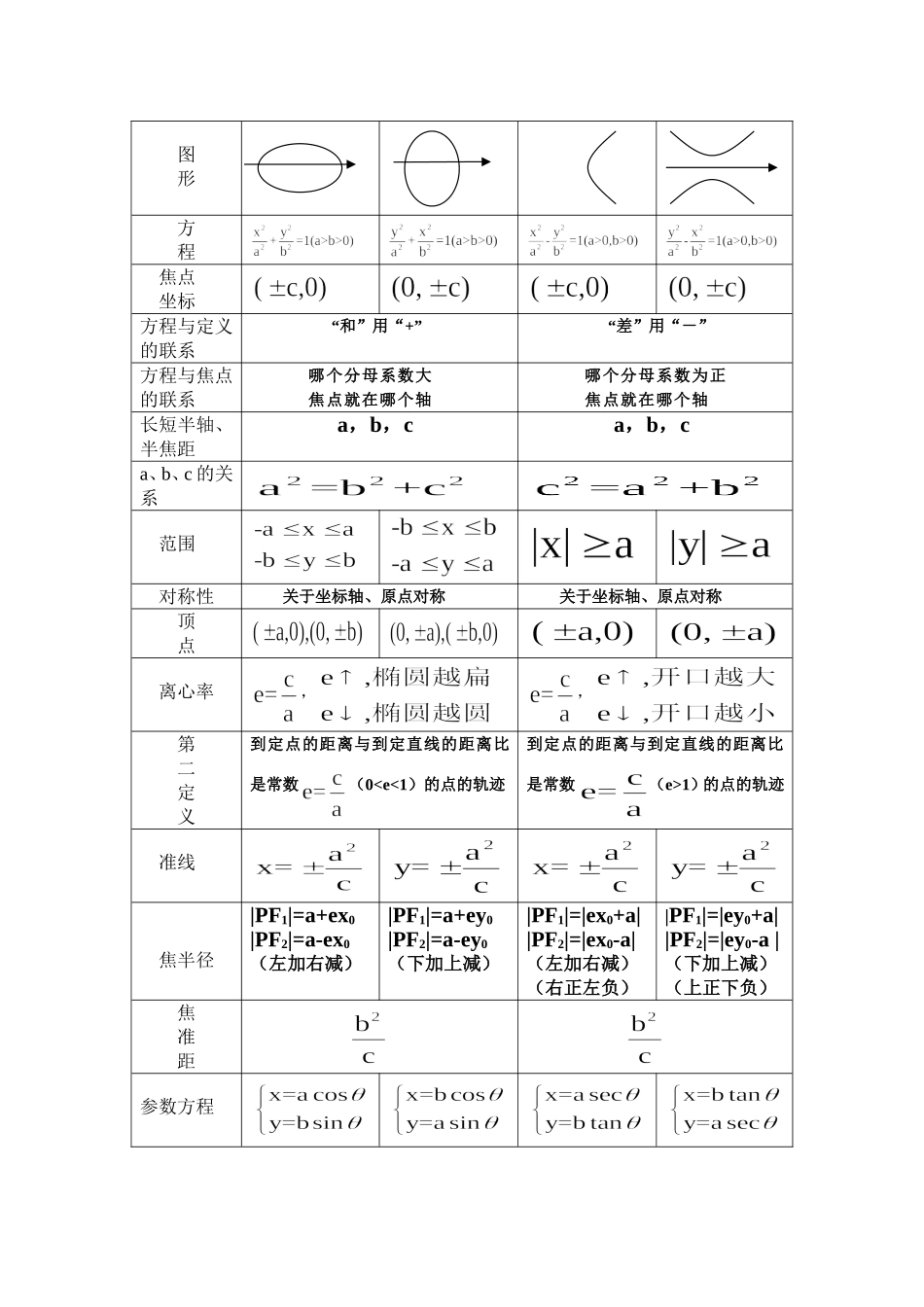
表一(定义探究)类比目标探究项目椭圆双曲线图形绘图原理绳子总长不变拉链拉开部分长度相等点集的文字描述平面内到两定点的距离的和等于常数(大于两定点的距离)点的集合平面内到两定点的距离的差的绝对值等于常数(小于两定点的距离)点的集合轨迹的点的集合|MF1|+|MF2|=2a(2a>2c)||MF1|-|MF2||=2a(2a<2c)方程推导建系设点以F1、F2所在直线为x轴,F1、F2中点为坐标原点建立坐标系,(如图)并设M(x,y)xyF2F1OM以F1、F2所在直线为x轴,F1、F2中点为坐标原点建立坐标系,(如图)并设M(x,y)xyF2F1OM列方程化简方程表二(性质探究)类比目标探究项目椭圆双曲线定义平面内到两定点的距离的和等于常数(大于两定点的距离)点的集合平面内到两定点的距离的差的绝对值等于常数(小于两定点的距离)点的集合图形方程焦点坐标方程与定义的联系“和”用“+”“差”用“-”方程与焦点的联系哪个分母系数大焦点就在哪个轴哪个分母系数为正焦点就在哪个轴长短半轴、半焦距a,b,ca,b,ca、b、c的关系范围对称性关于坐标轴、原点对称关于坐标轴、原点对称顶点离心率,,第二定义到定点的距离与到定直线的距离比是常数(01)的点的轨迹准线焦半径|PF1|=a+ex0|PF2|=a-ex0(左加右减)|PF1|=a+ey0|PF2|=a-ey0(下加上减)|PF1|=|ex0+a||PF2|=|ex0-a|(左加右减)(右正左负)|PF1|=|ey0+a||PF2|=|ey0-a|(下加上减)(上正下负)焦准距参数方程