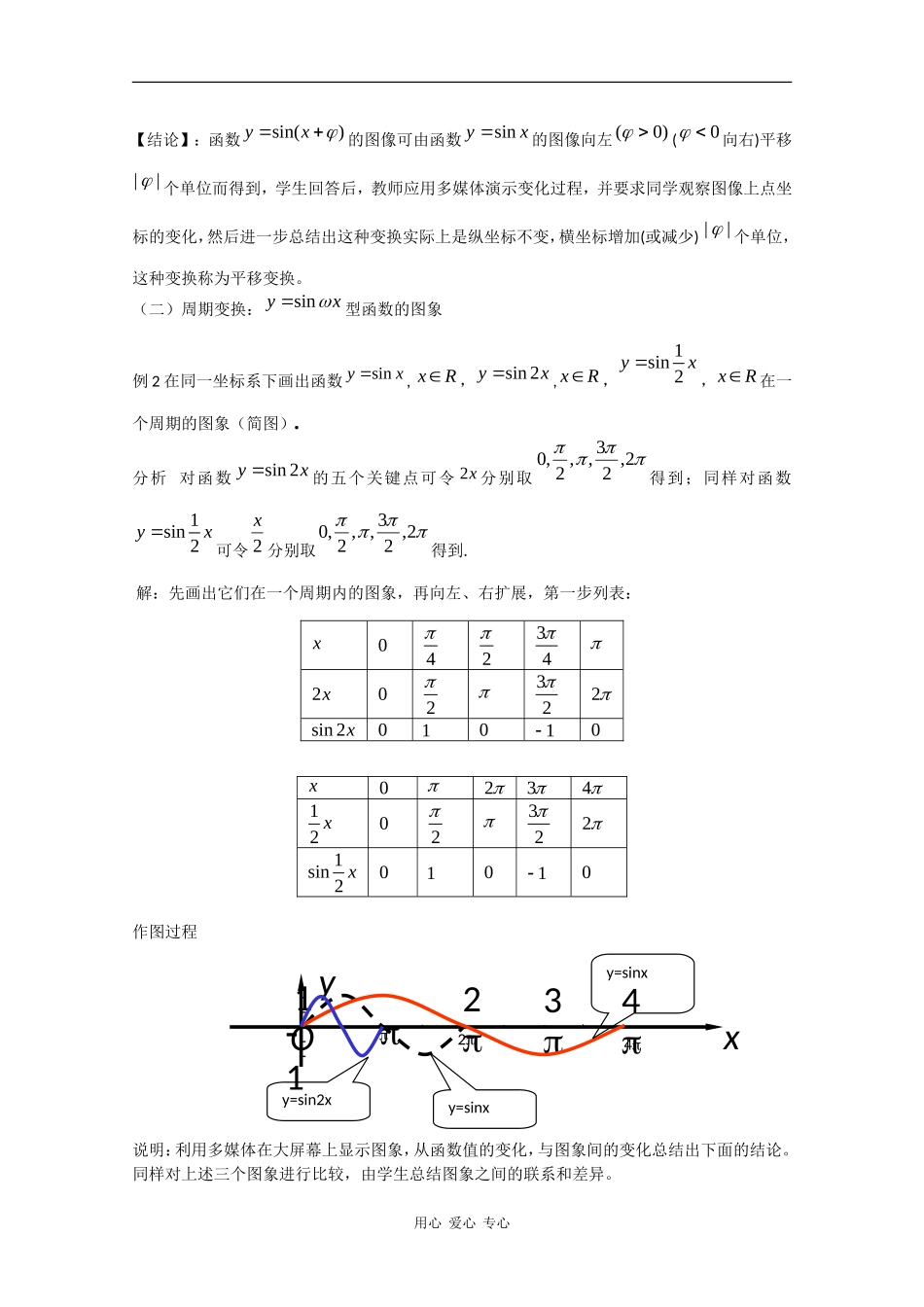
第12课时:1.3.3函数y=Asin(ωx+φ)的图象(一)【三维目标】:一、知识与技能1.结合具体实例,了解)sin(xAy的实际意义;能借助计算器或计算机画出)sin(xAy的图像,弄清参数,,A的物理意义及它们对函数sin()yAx的图象各有什么影响;2.理解振幅的定义及振幅变换和周期变换的规律,会画出xAysin、xysin、)sin(xy的图象;理解相位变换中的有关概念,会用相位变换画出函数的图象。二、过程与方法1.通过学生自己动手画图像,使他们知道列表、描点、连线是作图的基本要求;通过在同一个坐标平面内对比相关的几个函数图像,发现规律,总结提练,加以应用;要求学生能利用五点作图法,正确作出函数)sin(xAy的图像;讲解例题,总结方法,巩固练习。2.经历对函数xysin到)sin(xy的图象变换规律的探索过程,体会由简单到复杂,由特殊到一般的化归、数形结合的数学思想;3.在难点突破环节,培养学生全面分析、抽象、概括的能力;培养学生观察问题和探索问题的能力。三、情感、态度与价值观1.通过本节的学习,让学生认识动与静的辩证关系,学会运用运动变化的观点认识事物;2.创设问题情景,通过学生的亲身实践,引发学生学习兴趣,激发学生分析、探求的学习态度;3.让学生感受图形的对称美、运动美,培养学生对美的追求。【教学重点与难点】:重点:函数sin()yAx的图象以及参数,,A对函数的图象变化的影响;难点:)sin(xy的图象与xysin的关系;对周期变换、相位变换顺序不同,图象平移量也不同的理解;关键:理解三个参数A、ω、φ对函数)sin(xAy图象的影响。理解先进行周期变换时,图象的平移量为是突破本节课教学难点的关键.【学法与教学用具】:1.学法:自主探究、观察发现、合作交流、归纳总结。2.学法指导:在前面,我们知道精确度要求不高时,可以用五点作图法,是哪五个关键点?首先请同学们回忆,然后通过物理学中的几个情境引入课题;主要让学生动手实践,两节课尽可能多地让他们画图,教师只是加以点拨;可以从几个具体的、简单的例子开始,在适当的时候加以推广;先分解各个小知识点,再综合在一起,上升更高一层。以问题为载体,通过猜想、验证、证明的探究过程,掌握思考、讨论、交流的学习方法,并体验探究、发现和创造的乐趣.用心爱心专心3.教法:开放式探究、启发式引导、互动式讨论、反馈式评价“问题是数学的心脏”,本节课总体上以问题串的形式.着重抓几个探究点,突出学生的“探”、教师的“导”.并通过多媒体课件的演示,直观展示函数图象的变化过程,激发学生的学习兴趣.4.教学手段:运用多媒体网络教学平台,构建学生自主探究的教学环境。5.教学用具:多媒体、实物投影仪、三角板【授课类型】:新授课【课时安排】:1课时【教学思路】:一、创设情景,揭示课题1.复习提问:“五点法”作函数xysin简图的步骤,其中“五点”是指什么?2.引入函数)sin(xAy的物理背景;3.函数)0,0)(sin(AxAy的图象与xysin的图象有什么关系呢?二、研探新知,质疑答辩,排难解惑,发展思维(一)平移变换:sin()yx型的函数图象的作法例1作函数)3sin(xy和xysin的图象方法一:列表作图(学生用五点法列表画图)描点画图,思考上述两函数的图象五点差异.方法二:用平移法(注意讲清方向:“加左”“减右”)由)3sin(xy知可以看作将xysin的图象上各点向左平移3个单位得到一般地,函数sin()yx的图象和函数xysin图像的关系是什么?用心爱心专心x+302232x36326735sin(x+3)010-10yxO134y=sinxy=sin(x+)2【结论】:函数sin()yx的图像可由函数xysin的图像向左)0((0向右)平移||个单位而得到,学生回答后,教师应用多媒体演示变化过程,并要求同学观察图像上点坐标的变化,然后进一步总结出这种变换实际上是纵坐标不变,横坐标增加(或减少)||个单位,这种变换称为平移变换。(二)周期变换:sinyx型函数的图象例2在同一坐标系下画出函数xysin,xR,sin2yx,xR,1sin2yx,xR...