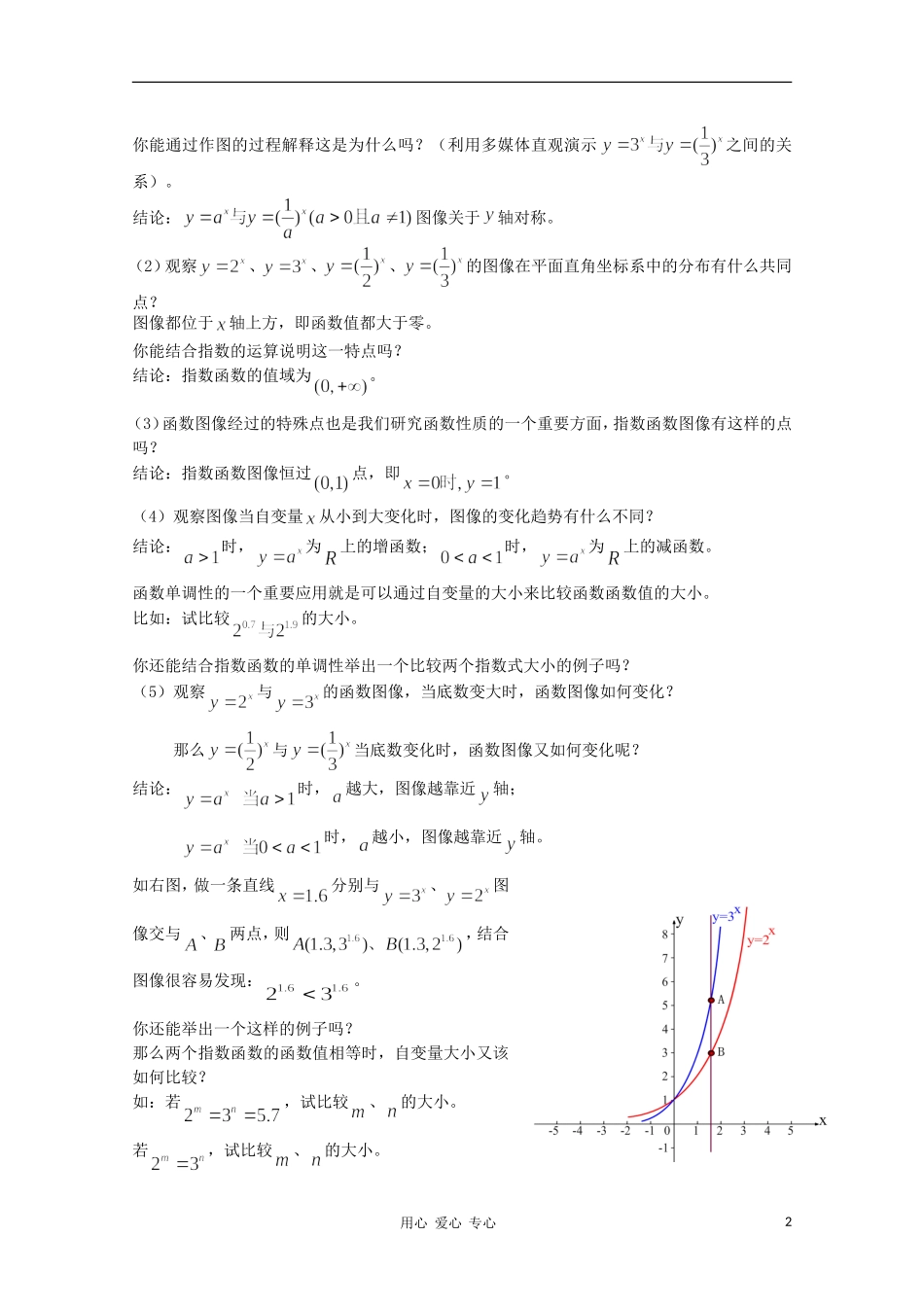
指数函数(一)教学目标:知识与技能:理解指数函数的概念和意义,掌握指数函数的图像和性质,并能自觉、灵活地应用其性质(单调性、底数变化图像的变化规律、中介值)比较大小。过程与方法:(1).体会从特殊到一般再到特殊的研究问题的方法,培养学生观察、猜想、归纳、概括的能力。(2).从数和形两方面理解指数函数的性质,体会数形结合、分类讨论的数学思想方法,提高思维的灵活性,培养学生直观、严谨的思维品质。情感、态度与价值观:(1).体验从特殊到一般再到特殊的学习规律,认识事物之间的普遍联系与相互转化,培养学生用联系的观点看问题,激发学生自主探究的精神,在探究过程中体验合作学习的乐趣。(2).让学生在数形结合中感悟数学的统一美、和谐美,进一步培养学生的学习兴趣。教学重点:指数函数的图像和性质。教学难点:指数函数的底数对图像的影响。教学过程:(一)、概念引入:1.某种细胞分裂时,由一个分裂成两个,两个分裂成四个,四个分裂成八个,以此类推,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系式是什么?2.一种放射性物质不断变化为其它物质,每经过一年剩余质量约是原来的,设该物质的初始质量为1,经过年后的剩余质量为,你能写出之间的函数关系式吗?1.2.上述两个函数都是正整数指数函数,但在实际问题中指数不一定都是正整数,比如在实例(2)中,我们除了关心1年、2年、3年后该物质的剩余量外,还想知道3个月、一年半后该物质的剩余量,这就需要对正整数指数函数的定义域进行扩充,结合指数概念的的扩充,我们也可以将正整数指数函数的定义域扩充至全体实数,这样就得到了一个新的函数——指数函数。一般地,函数叫做指数函数,其中。结合指数的运算,引导学生分析为什么规定,加深学生对概念的理解。你能举出指数函数的例子吗?练习1:判断下列函数是否为指数函数。(1)(2)(3)(4)(二)、通过图像探究指数函数的性质及其简单应用:(1)用描点法作与的图像,并观察图像之间的关系:图像关于y轴对称。用心爱心专心1你能通过作图的过程解释这是为什么吗?(利用多媒体直观演示之间的关系)。结论:图像关于轴对称。(2)观察、、、的图像在平面直角坐标系中的分布有什么共同点?图像都位于轴上方,即函数值都大于零。你能结合指数的运算说明这一特点吗?结论:指数函数的值域为。(3)函数图像经过的特殊点也是我们研究函数性质的一个重要方面,指数函数图像有这样的点吗?结论:指数函数图像恒过点,即。(4)观察图像当自变量从小到大变化时,图像的变化趋势有什么不同?结论:时,为上的增函数;时,为上的减函数。函数单调性的一个重要应用就是可以通过自变量的大小来比较函数函数值的大小。比如:试比较的大小。你还能结合指数函数的单调性举出一个比较两个指数式大小的例子吗?(5)观察与的函数图像,当底数变大时,函数图像如何变化?那么与当底数变化时,函数图像又如何变化呢?结论:时,越大,图像越靠近轴;时,越小,图像越靠近轴。如右图,做一条直线分别与、图像交与、两点,则,结合图像很容易发现:。你还能举出一个这样的例子吗?那么两个指数函数的函数值相等时,自变量大小又该如何比较?如:若,试比较、的大小。若,试比较、的大小。用心爱心专心2你还能举出这样的例子吗?(6)观察、的图像与直线有什么关系呢?轴右侧的图像在直线的上方,轴左侧的图像在直线的下方。结论:当时,;当时,。由、的图像与直线的关系你又能得出什么结论呢?结论:当时,;当时,。试用上述性质比较的大小。你还能举出这样的例子吗?(7)、指数函数性质归纳小结:(三)、课堂小结:(1)、理解指数函数的概念,掌握指数函数的图像和性质,并能自觉、灵活地应用其性质比较大小。(2)、研究函数的一般方法:解析式图像性质。(2)、体会从特殊到一般再到特殊的研究问题的方法,以及数形结合、分类讨论的数学思想。(四)、布置作业:(1)、课本第3、4题。(2)、搜集指数函数在实际生活中的应用实例。指数函数(一)教案说明三原南郊中学柏涛一、授课内容的数学本质及教学目标定位:《指数函数》是北师大版高中数学必修(...