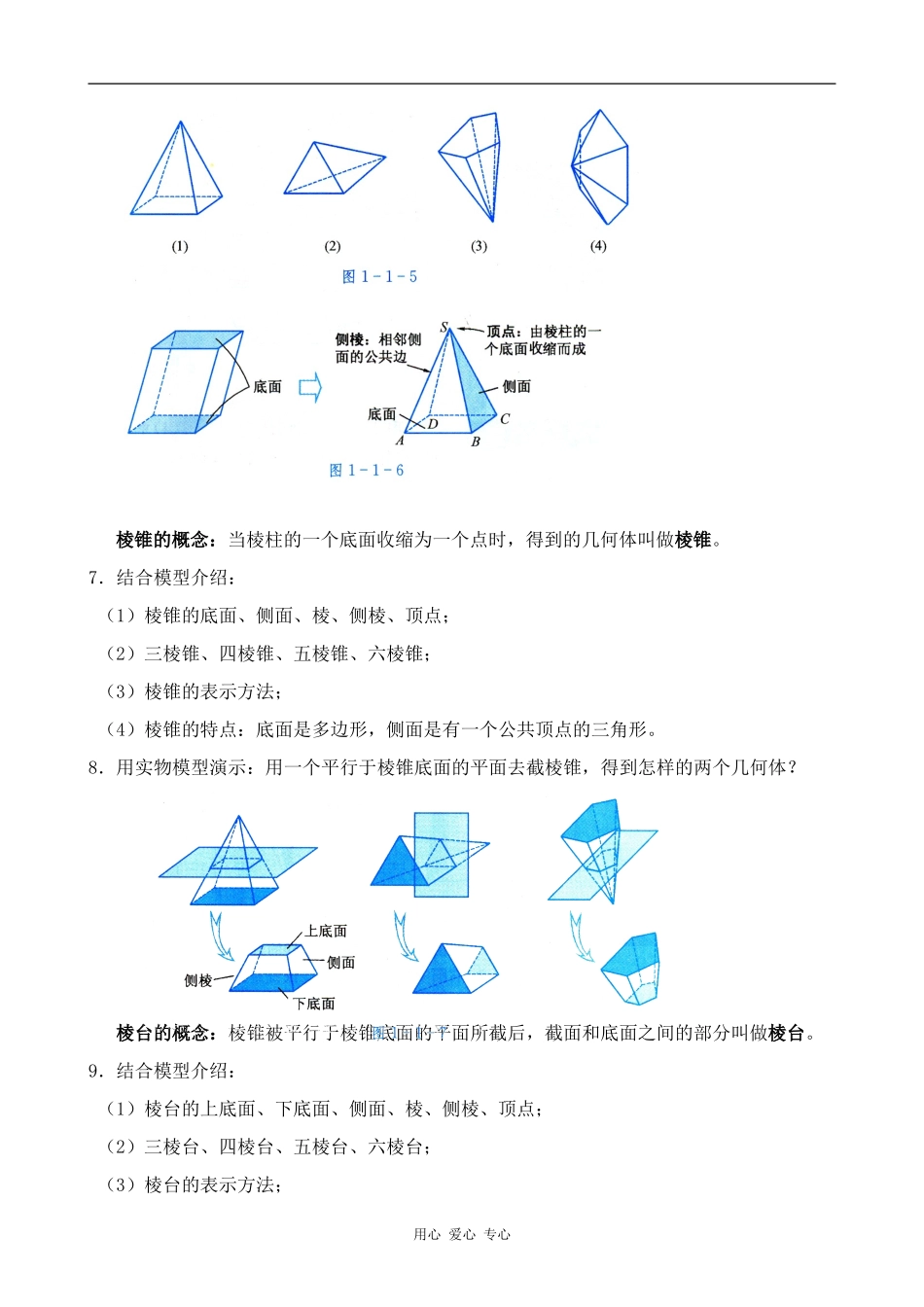
棱柱、棱锥和棱台教学目标(1)感知并认识棱柱、棱锥和棱台的结构特征,初步形成空间观念;(2)了解棱柱、棱锥和棱台的概念,能画出棱柱、棱锥和棱台的示意图;(3)能用运动变化的观点认识棱柱、棱锥和棱台的辨证关系.教学重点棱柱、棱锥和棱台的结构特征和有关概念.教学难点棱柱、棱锥和棱台的结构特征.教学过程一、问题情境1.情境:(1)阅读章头图和本章引言。意图:使学生了解学习立体几何的必要性,了解本章主要解决什么问题。(2)给出多种棱柱的实物模型,让学生观察。2.问题:仔细观察这些几何体,说说他们的共同特点.二、学生活动学生讨论,归纳:有两个面是全等的多边形,其余各面都是平行四边形。教师:这样的几何体称为棱柱。三、建构数学1.在水平地面上有不同的两点和,一只蜗牛沿到方向从点爬到点,留下怎样的痕迹?线段;由此可见,点从一个位置沿某一确定的方向平移到另一位置,形成怎样的图形?线段。2.把一支粉笔贴在黑板上,沿垂直于粉笔的方向平移,留下怎样的痕迹?(演示)矩形;由此可见,一条线段从一个位置沿某一确定的方向平移到另一位置,形成怎样的图形?平行四边形。3.把一张矩形纸片放在课桌上,向上平移,形成怎样的图形?用心爱心专心操作:堆课本。(课本的纸张大小相同)长方体。4.一般地,由一个平面多边形沿某一方向平移形成怎样的空间几何体?用电脑演示平移多边形生成棱柱的过程。棱柱的概念:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱。平移起、止位置的两个面叫做棱柱的底面,多边形的边平移所形成的面叫做棱柱的侧面。5.结合模型介绍:(1)棱柱的底面、侧面、棱、侧棱、顶点;(2)三棱柱、四棱柱、五棱柱、六棱柱;(3)棱柱的表示方法;(4)棱柱的特点:两个底面是全等的多边形,且对应边互相平行,侧面都是平行四边形。6.给出一组棱锥,让学生将它们与棱柱进行比较,前后发生了什么变化?棱柱的一个底面收缩为一个点时,得到相应的棱锥。用电脑演示棱柱的一个底面收缩为一个点生成棱柱的过程。用心爱心专心棱锥的概念:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥。7.结合模型介绍:(1)棱锥的底面、侧面、棱、侧棱、顶点;(2)三棱锥、四棱锥、五棱锥、六棱锥;(3)棱锥的表示方法;(4)棱锥的特点:底面是多边形,侧面是有一个公共顶点的三角形。8.用实物模型演示:用一个平行于棱锥底面的平面去截棱锥,得到怎样的两个几何体?棱台的概念:棱锥被平行于棱锥底面的平面所截后,截面和底面之间的部分叫做棱台。9.结合模型介绍:(1)棱台的上底面、下底面、侧面、棱、侧棱、顶点;(2)三棱台、四棱台、五棱台、六棱台;(3)棱台的表示方法;用心爱心专心(4)棱台的特点:两个底面是相似多边形,侧面都是梯形;侧棱延长后交于一点。10.结合模型介绍:由若干个平面多边形围成的几何体叫做多面体。多面体有几个面就称为几面体。如:三棱锥是四面体,四棱柱是六面体。四、回顾小结:1.本节课学习了棱柱、棱锥和棱台的概念,以及棱柱、棱锥和棱台示意图的画法;2.棱柱、棱锥和棱台有怎样的辨证关系?3.空间图形中,实线和虚线分别表示什么?作辅助线时,要注意什么?五、作业:1.设计一个平面图形,使它能够折成一个侧面与底面都是正三角形的三棱锥。2.下列几何体是否是棱台?为什么?用心爱心专心(1)(2)