高中数学对数函数——对数函数的定义、图象、性质苏教版必修一VIP免费

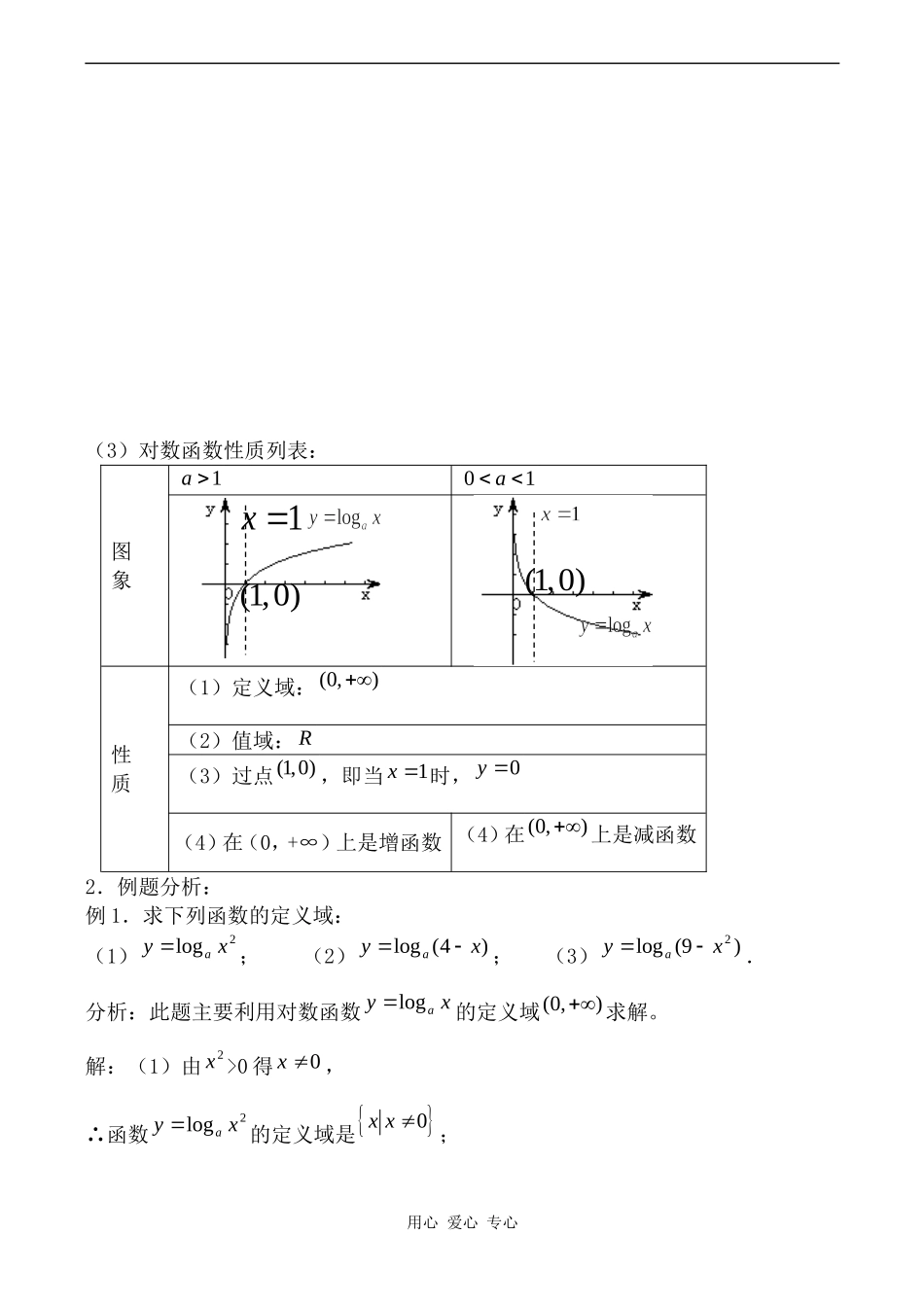
对数函数——对数函数的定义、图象、性质一．课题：对数函数——对数函数的定义、图象、性质二．教学目标：1．要求学生了解对数函数的定义、图象及其性质以及它与指数函数间的关系2．明确对数函数与指数函数的互为反函数，能利用其相互关系研究问题，会求对数函数的定义域；3．记住对数函数图象的规律，并能用于解题；4．培养培养学生数形结合的意识用联系的观点研究数学问题的能力。三．教学重点：对数函数的图象和性质，能熟练地求与对数函数有关的函数的定义域。四．教学难点：对数函数与指数函数的关系，借助指数函数研究对数函数的图象和性质。五．教学过程：（一）复习引入：1．指数函数的定义、图象、性质。2．回忆学习指数函数时的实例——细胞分裂问题：细胞的个数是分裂次数的指数函数xy2．反之，细胞分裂的次数是细胞个数的函数，由对数定义：yx2log，即：次数y是个数x的函数xy2log．（二）新课讲解：1．对数函数的定义：函数xyalog)10(aa且叫做对数函数。2．对数函数的性质：（1）定义域、值域：对数函数xyalog)10(aa且的定义域为),0(，值域为),(．（2）图象：由于对数函数是指数函数的反函数，所以对数函数的图象只须由相应的指数函数图象作关于xy的对称图形，即可获得。同样：也分1a与10a两种情况归纳，以xy2log（图1）与xy21log（图2）为例。用心爱心专心112xy2logyxyx（图1）111()2xy12logyxyx（图2）（3）对数函数性质列表：图象1a01a性质（1）定义域：(0,)（2）值域：R（3）过点(1,0)，即当1x时，0y（4）在（0，+∞）上是增函数（4）在(0,)上是减函数2．例题分析：例1．求下列函数的定义域：（1）2logxya；（2）)4(logxya；（3）)9(log2xya．分析：此题主要利用对数函数xyalog的定义域(0,)求解。解：（1）由2x>0得0x，∴函数2logxya的定义域是0xx；用心爱心专心(1,0)(1,0)1x（2）由04x得4x，∴函数)4(logxya的定义域是4xx；（3）由9-02x得-33x，∴函数)9(log2xya的定义域是33xx．说明：此题只是对数函数性质的简单应用，应强调学生注意书写格式。例2．求函数251xy和函数22112xy)0(x的反函数。解：（1）125xy∴115()log(2)fxx(-2)x；（2）211-22xy∴-112()log(-2)fxx5(2)2x．例3．作出下列函数的图象：（1）2log||yx（2）12|log(2)|yx．分析：本题主要利用函数图象的平移、对称变换来作图（图略）。用心爱心专心