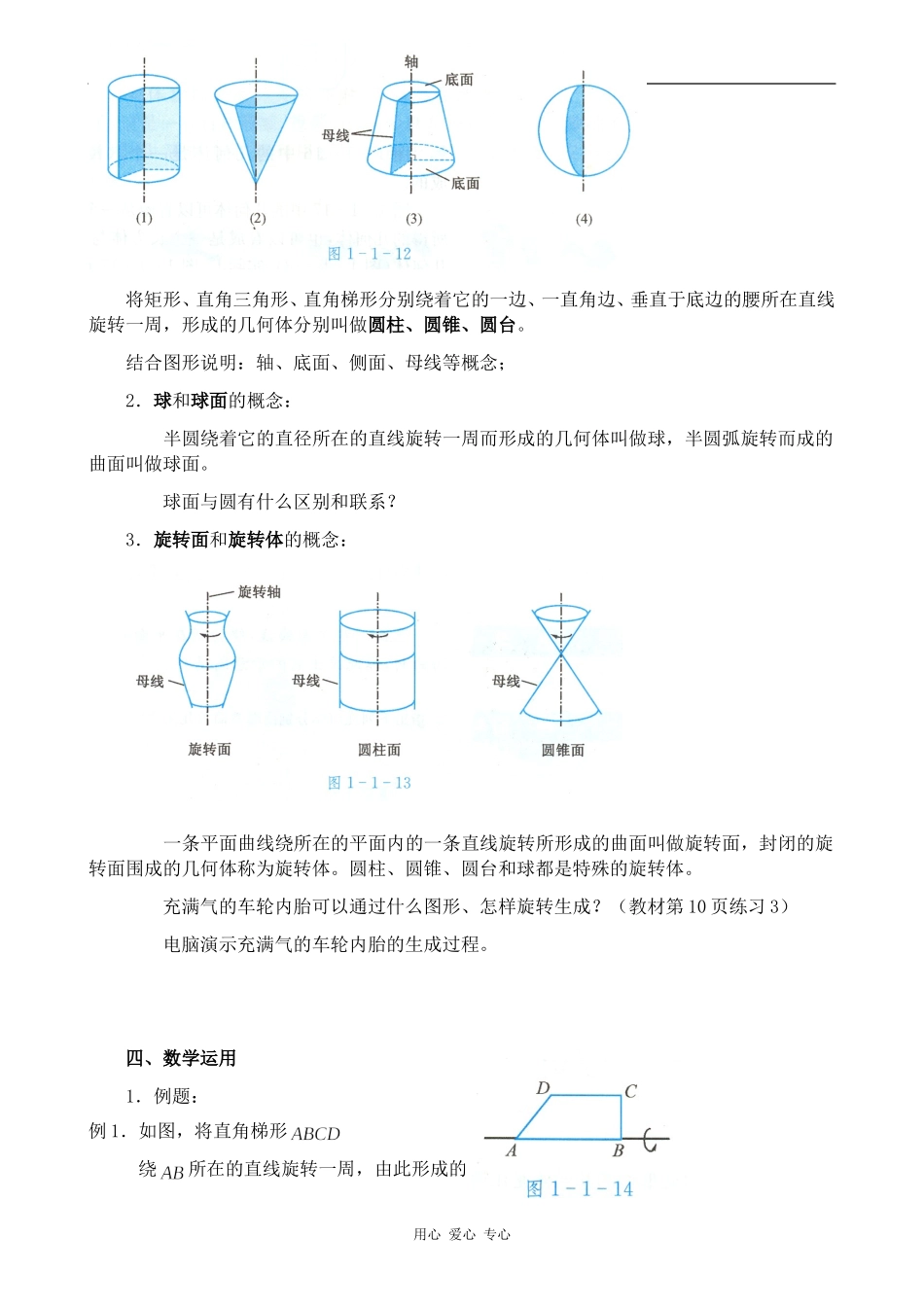
圆柱、圆锥、圆台和球教学目标(1)感知并认识圆柱、圆锥、圆台和球的结构特征,初步形成空间观念;(2)了解圆柱、圆锥、圆台和球的概念,初步理解旋转体的概念;(3)能判断组合体是由哪些简单几何体构成的,培养学生的识图能力与空间想象能力.教学重点圆柱、圆锥、圆台和球的结构特征和有关概念.教学难点判断组合体是由哪些简单几何体构成的.教学过程一、问题情境1.复习棱柱、棱锥和棱台的概念;2.给出圆柱、圆锥、圆台和球的实物模型,让学生观察。3.问题:仔细观察这些几何体,类比上节课的内容,说说他们的共同特点或生成规律.二、学生活动1.学生讨论,归纳:圆柱可以看成圆面沿着圆面的铅垂方向平移形成的空间几何体;圆锥可以看成当圆柱的一个底面收缩为圆心时,得到的几何体;圆台可以看成圆锥被平行于圆锥底面的平面所截后,截面和底面之间的部分。2.问题:这类几何体往往可以在车床上通过旋转切割加工得到,它们都可以看成由一个平面图形绕一条直线旋转而生成的。你能想象它们分别是什么平面图形通过旋转而生成的吗?教师用电脑演示旋转生成圆柱、圆锥、圆台和球的过程。教师:这样的几何体称为旋转体。三、建构数学1.圆柱、圆锥、圆台的概念:用心爱心专心将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、垂直于底边的腰所在直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台。结合图形说明:轴、底面、侧面、母线等概念;2.球和球面的概念:半圆绕着它的直径所在的直线旋转一周而形成的几何体叫做球,半圆弧旋转而成的曲面叫做球面。球面与圆有什么区别和联系?3.旋转面和旋转体的概念:一条平面曲线绕所在的平面内的一条直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体称为旋转体。圆柱、圆锥、圆台和球都是特殊的旋转体。充满气的车轮内胎可以通过什么图形、怎样旋转生成?(教材第10页练习3)电脑演示充满气的车轮内胎的生成过程。四、数学运用1.例题:例1.如图,将直角梯形绕所在的直线旋转一周,由此形成的几用心爱心专心何体是由哪些简单几何体构成的?例2.指出下图中的几何体是由哪些简单几何体构成的?五、回顾小结:1.本节课学习了圆柱、圆锥、圆台和球的概念;2.圆柱、圆锥和圆台球怎样的辨证关系?3.棱柱、棱锥、棱台和圆柱、圆锥、圆台、球都是简单几何体,要能通过分析组合体的结构特征,分辨出组合体是哪些简单几何体构成的。六、课外作业:1.已知如图所示的直角梯形,说出它分别绕直线、、旋转所形成的几何体的名称(或由哪些简单几何体构成的),并画出相应几何体的大致形状。2.分别用一个经过轴的平面去截圆柱、圆锥和圆台,截面各是什么多边形?该多边形的各边与相应的几何体有何联系?3.下图第一行中的六个图形绕虚线旋转一周,能形成第二行中的某个几何体,请写出它们的对应来。用心爱心专心DCBA用心爱心专心