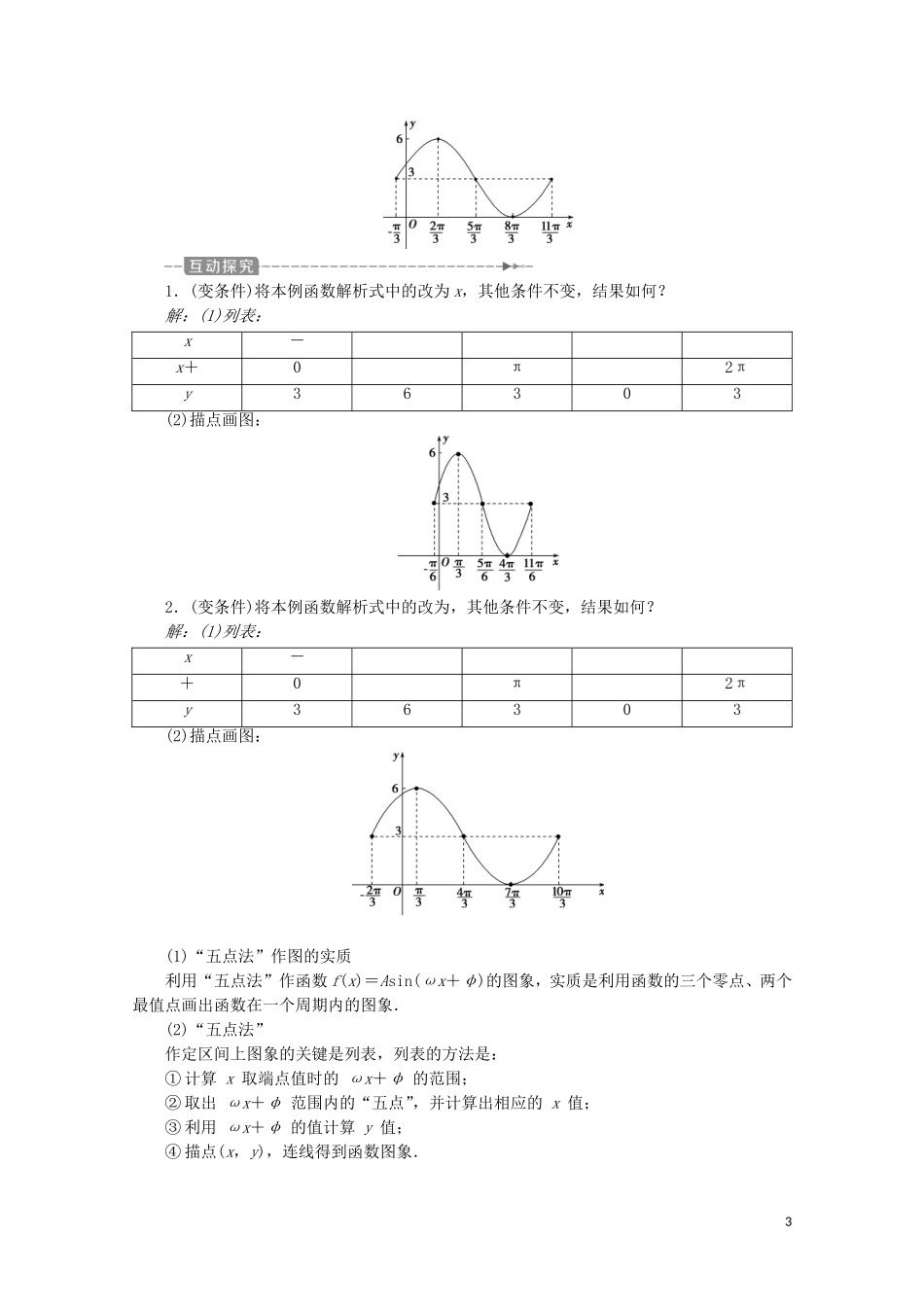
第1课时函数y=Asin(ωx+φ)的图象及变换考点学习目标核心素养“五点法”作图会用“五点法”作函数y=Asin(ωx+φ)的图象直观想象三角函数的图象变换会通过变换由y=sinx的图象得到y=Asin(ωx+φ)的图象逻辑推理、直观想象问题导学预习教材P231-P239,并思考以下问题:1.如何用y=sinx的图象变换为y=sin(x+φ)(其中φ≠0)的图象?2.如何用y=sinx的图象变换为y=Asinx(A>0且A≠1)的图象?3.如何用y=sinx的图象变换为y=sinωx(ω>0且ω≠1)的图象?A、ω、φ对函数y=Asin(ωx+φ)的图象的影响(1)φ对函数y=sin(x+φ)的图象的影响―→(2)ω(ω>0)对函数y=sin(ωx+φ)的图象的影响(3)A(A>0)对函数y=Asin(ωx+φ)的图象的影响■名师点拨A,ω,φ对函数y=Asin(ωx+φ)的图象的影响(1)A越大,函数图象的最大值越大,最大值与A是正比例关系.1(2)|ω|越大,函数图象的周期越小,|ω|越小,周期越大,周期与|ω|为反比例关系.(3)φ>0时,函数图象向左平移,φ<0时,函数图象向右平移,即“加左减右”.判断正误(正确的打“√”,错误的打“×”)(1)将函数y=sinx的图象向左平移个单位,得到函数y=cosx的图象.()(2)将函数y=sinx图象上各点的纵坐标变为原来的2倍,便得到函数y=2sinx的图象.()(3)把函数y=cosx图象上各点的横坐标伸长到原来的3倍就得到函数y=cos3x的图象.()答案:(1)√(2)√(3)×利用“五点法”作函数y=sinx,x∈[0,2π]的图象时,所取的五点的横坐标为()A.0,,π,,2πB.0,,,,πC.0,π,2π,3π,4πD.0,,,,答案:C将函数y=cosx图象上各点的纵坐标伸长为原来的4倍,横坐标不变,得到的函数解析式为()A.y=4cosxB.y=2cosxC.y=cosxD.y=cosx答案:B要得到函数y=sin的图象,可以将函数y=sinx的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度答案:B将函数y=sinx的图象上所有点的横坐标缩短到原来的倍(纵坐标不变)得________的图象.答案:y=sin4x“五点法”作图已知函数y=3sin+3(x∈R),用“五点法”画出它在一个周期内的闭区间上的图象.【解】(1)列表:x-+0π2πy36303(2)描点画图:21.(变条件)将本例函数解析式中的改为x,其他条件不变,结果如何?解:(1)列表:x-x+0π2πy36303(2)描点画图:2.(变条件)将本例函数解析式中的改为,其他条件不变,结果如何?解:(1)列表:x-+0π2πy36303(2)描点画图:(1)“五点法”作图的实质利用“五点法”作函数f(x)=Asin(ωx+φ)的图象,实质是利用函数的三个零点、两个最值点画出函数在一个周期内的图象.(2)“五点法”作定区间上图象的关键是列表,列表的方法是:①计算x取端点值时的ωx+φ的范围;②取出ωx+φ范围内的“五点”,并计算出相应的x值;③利用ωx+φ的值计算y值;④描点(x,y),连线得到函数图象.3用“五点法”作出函数y=2sin+3的图象.解:①列表如下:xππππx-0ππ2πy35313②描点.③连线成图.将这个函数在一个周期内的图象向左、右两边扩展即得y=2sin+3的图象.如图所示.三角函数的图象变换(1)有下列四种变换方式:①向左平移个单位长度,再将横坐标变为原来的(纵坐标不变);②横坐标变为原来的(纵坐标不变),再向左平移个单位长度;③横坐标变为原来的(纵坐标不变),再向左平移个单位长度;④向左平移个单位长度,再将横坐标变为原来的(纵坐标不变).其中能将正弦函数y=sinx的图象变为y=sin的图象的是()A.①和②B.①和③C.②和③D.②和④(2)(2018·高考天津卷改编)将函数y=sin的图象向右平移个单位长度,所得图象对应的函数解析式为__________.【解析】(1)①向左平移个单位长度,再将横坐标变为原来的(纵坐标不变),则正弦函数y=sinx的图象变为y=sin的图象;②横坐标变为原来的(纵坐标不变),再向左平移个单位长度,正弦函数y=sinx的图象变为y=sin2=sin的图象;③横坐标变为原来的(纵坐标不变),再向左平移个单位长度,正弦函数y=sinx的图象变为y=sin2=sin的图象;④向左平移个单位长度,再将横坐标变为原来的(纵坐标不变),正弦函数y=sinx的图象变为y...