高中数学 第三章指数函数与对数函数复习一教案 北师大版必修1VIP免费

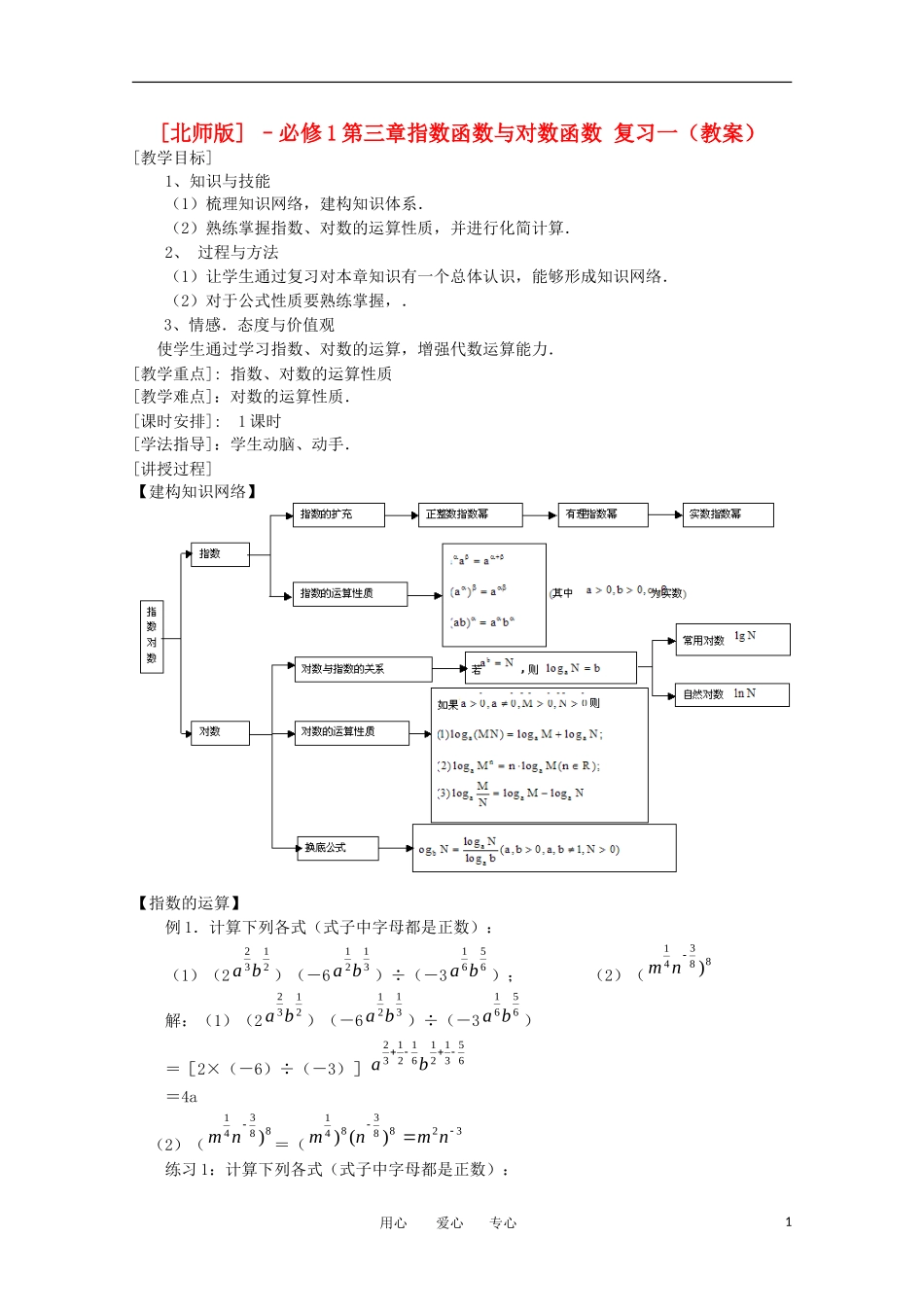
[北师版]–必修1第三章指数函数与对数函数复习一（教案）[教学目标]1、知识与技能（1）梳理知识网络，建构知识体系．（2）熟练掌握指数、对数的运算性质，并进行化简计算．2、过程与方法（1）让学生通过复习对本章知识有一个总体认识，能够形成知识网络．（2）对于公式性质要熟练掌握，．3、情感．态度与价值观使学生通过学习指数、对数的运算，增强代数运算能力．[教学重点]:指数、对数的运算性质[教学难点]：对数的运算性质．[课时安排]:1课时[学法指导]：学生动脑、动手．[讲授过程]【建构知识网络】【指数的运算】例1．计算下列各式（式子中字母都是正数）：（1）（22132ba）（－63121ba）÷（－36561ba）；（2）（88341)nm解：（1）（22132ba）（－63121ba）÷（－36561ba）＝［2×（－6）÷（－3）］653121612132ba＝4a（2）（88341)nm＝（32883841)()nmnm练习1：计算下列各式（式子中字母都是正数）：用心爱心专心11153322(1)(4xy)(3xy)；11143223332(2)(2mn)(3mn)(mn)【根式的运算】例2．计算下列各式：（1）4325)12525(；（2）322aaa（a＞0）解：（1）4325)12525(＝55556121232132＝65－5（2）322aaa（a＞0）＝6532212aa＝65a练习2：．计算下列各式：2323(1)xyxy；34(2)321288【对数的运算】例3．计算：log12（3＋22）的值．解：log12（3＋22）=12(21)(21)log(21)2log(21)2例4．已知lgx=a，lgy=b，lgz=c，且有a＋b＋c=0，求xcb11·yac11·xba11的值．解：．由lgx=a，lgy=b，lgz=c，得x=10a，y=10b，z=10c，所以xcb11·yac11·xba11=10)()()(cacbbabcacab=10111=03=10001．练习3：（1）．已知log2[log21（log2x）]=log3[log31（log3y）]=log5[log51（log5z）]=0，试比较x、y、z的大小．解：由log2[log21（log2x）]=0得，log21（log2x）=1，log2x=21，即x=221；由log3[log31（log3y）]=0得，log31（log3y）=1，log3y=31，即y=331；由log5[log51（log5z）]=0得，log51（log5z）=1，log5z=51，即z=551．∵y=331=362=961，∴x=221=263=861，∴y＞x，用心爱心专心2又∵x=221=2105=32101，z=551=5102=25101，∴x＞z．故y＞x＞z．（2）．设a，b为正数，且a2－2ab－9b2=0，求lg（a2＋ab－6b2）－lg（a2＋4ab＋15b2）的值．解:由a2－2ab－9b2=0，得（ba）2－2（ba）－9=0，令ba=x＞0，∴x2－2x－9=0，解得x=1＋10，（舍去负根），且x2=2x＋9，∴lg（a2＋ab－6b2）－lg（a2＋4ab＋15b2）=lg22221546babababa=lg154622xxxx=lg154)92(6)92(xxxx=lg)4(6)1(3xx=lg)4(21xx=lg)4101(21101=lg1010=－21．作业：复习题三A组1-4用心爱心专心3