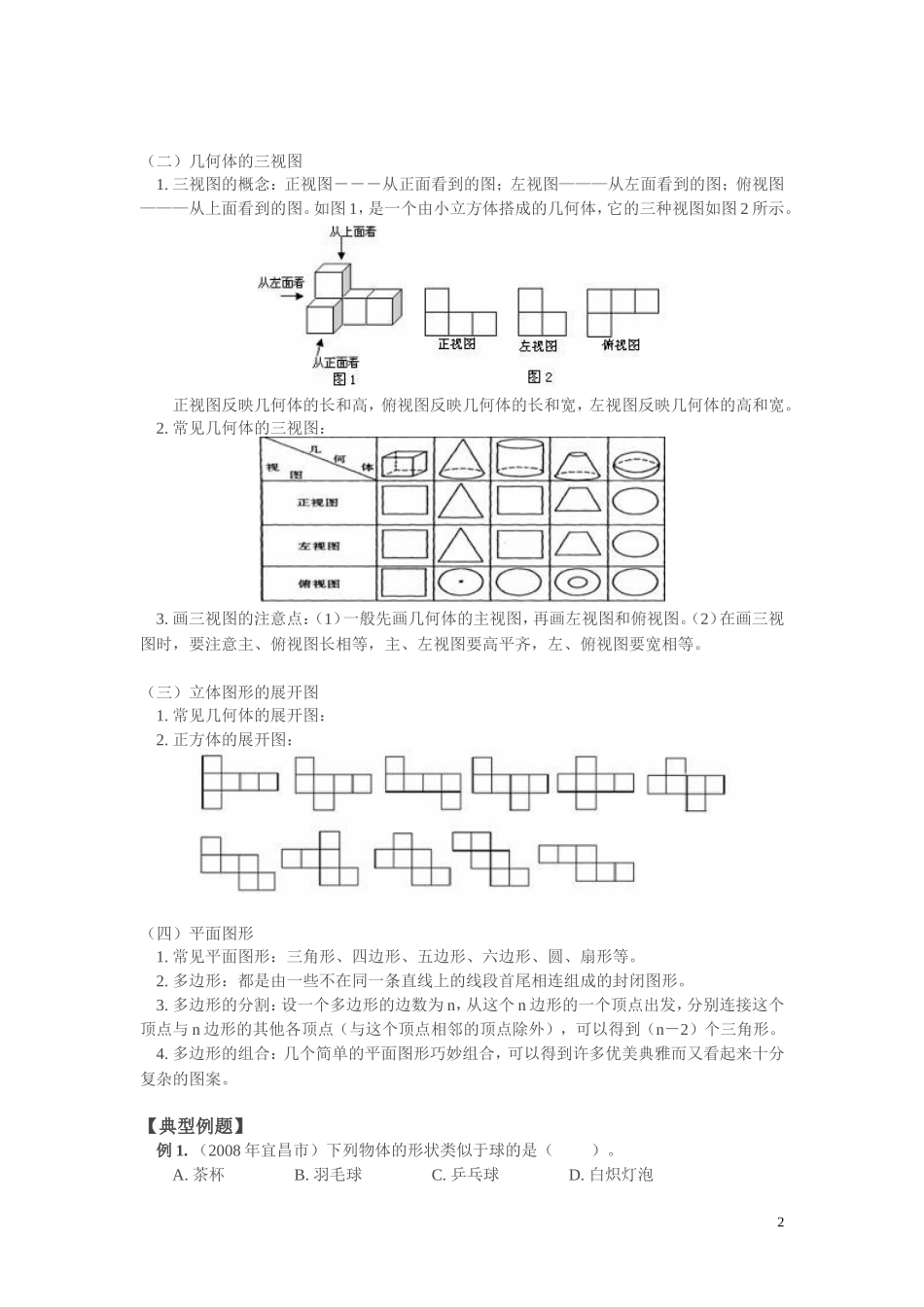
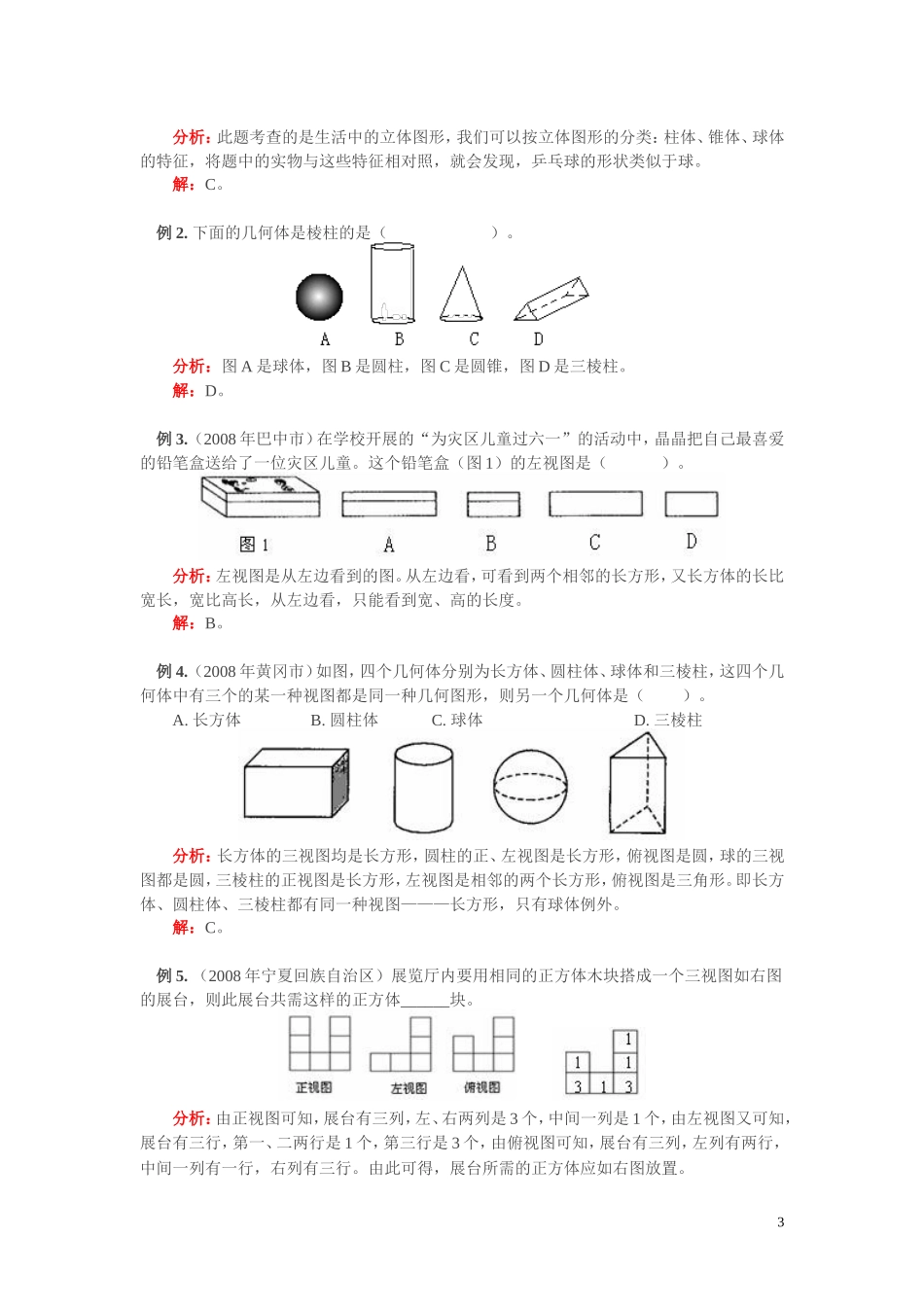
高中数学正方体展开图问题教案新人教A版必修2一.本周教学内容:从立体图形到平面图形二.知识要点:1.知识点概要⑴认识圆柱、圆锥、棱柱、球等立体图形的特征,能对几何体进行分类。⑵能识别简单物体的三视图,会画简单几何体的三视图,并能根据三视图想象几何体或实物原形。⑶认识立体图形与平面图形的关系,经历和体验图形的变化过程,掌握棱柱、圆锥、圆柱的侧面展开图,能根据展开图想象立体模型。尤其是掌握正方体的展开与折叠。⑷了解多边形的概念,知道任何多边形都可由三角形组合而成,知道点、线、多边形、圆等图形可组合成各种优美的图案。2.重点难点⑴重点:对几何体的识别及分类,简单物体的三视图,根据展开图想象和制作立体模型。⑵难点:由实物的形状抽象出几何图形,由几何图形想象出实物的形状,进行几何体与其三视图、展开图之间的相互转化。三.考点分析:(一)立体图形1.常见几何体的类型:①柱体;②锥体;③球体。如图所示:图⑵,⑷,⑸,⑹,⑺都称为柱体,它们有两个面互相平行,余下的每相邻两个面的交线互相平行。图⑴,⑼,⑽都称为锥体,图⑶是球体。由图可以看出,柱体包括圆柱、棱柱;锥体包括圆锥、棱锥。2.常见几何体的特征:棱柱:棱柱的所有侧棱都相等,侧面的形状都是长方形,棱柱的上、下底面的形状相同。因底面的形状不同而分为三棱柱,四棱柱、五棱柱……,如图⑷,⑸,是四棱柱,⑹是三棱柱,⑺是五棱柱。圆柱:上、下底面是半径相等的两个圆面,侧面是一个曲面。如图⑵。棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形。因底面的形状不同而分为三棱锥,四棱锥、五棱锥……,如图⑼是四棱锥,图⑽是三棱锥。圆锥:由一个底面(为圆)和一个侧面组成。3.多面体:由多个平面围成的密封的几何体。如果把一个多面体具有的顶点数记作V,棱数记作E,面数记作F,通过观察简单的多面体得到V+F-E=2,即顶点数+面数-棱数=2,人们称它为欧拉公式。1(二)几何体的三视图1.三视图的概念:正视图―――从正面看到的图;左视图———从左面看到的图;俯视图———从上面看到的图。如图1,是一个由小立方体搭成的几何体,它的三种视图如图2所示。正视图反映几何体的长和高,俯视图反映几何体的长和宽,左视图反映几何体的高和宽。2.常见几何体的三视图:3.画三视图的注意点:(1)一般先画几何体的主视图,再画左视图和俯视图。(2)在画三视图时,要注意主、俯视图长相等,主、左视图要高平齐,左、俯视图要宽相等。(三)立体图形的展开图1.常见几何体的展开图:2.正方体的展开图:(四)平面图形1.常见平面图形:三角形、四边形、五边形、六边形、圆、扇形等。2.多边形:都是由一些不在同一条直线上的线段首尾相连组成的封闭图形。3.多边形的分割:设一个多边形的边数为n,从这个n边形的一个顶点出发,分别连接这个顶点与n边形的其他各顶点(与这个顶点相邻的顶点除外),可以得到(n-2)个三角形。4.多边形的组合:几个简单的平面图形巧妙组合,可以得到许多优美典雅而又看起来十分复杂的图案。【典型例题】例1.(2008年宜昌市)下列物体的形状类似于球的是()。A.茶杯B.羽毛球C.乒乓球D.白炽灯泡2分析:此题考查的是生活中的立体图形,我们可以按立体图形的分类:柱体、锥体、球体的特征,将题中的实物与这些特征相对照,就会发现,乒乓球的形状类似于球。解:C。例2.下面的几何体是棱柱的是()。分析:图A是球体,图B是圆柱,图C是圆锥,图D是三棱柱。解:D。例3.(2008年巴中市)在学校开展的“为灾区儿童过六一”的活动中,晶晶把自己最喜爱的铅笔盒送给了一位灾区儿童。这个铅笔盒(图1)的左视图是()。分析:左视图是从左边看到的图。从左边看,可看到两个相邻的长方形,又长方体的长比宽长,宽比高长,从左边看,只能看到宽、高的长度。解:B。例4.(2008年黄冈市)如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是()。A.长方体B.圆柱体C.球体D.三棱柱分析:长方体的三视图均是长方形,圆柱的正、左视图是长方形,俯视图是圆,球的三视图...