高中数学 指数函数与对数函数复习教案 苏教版必修1VIP免费

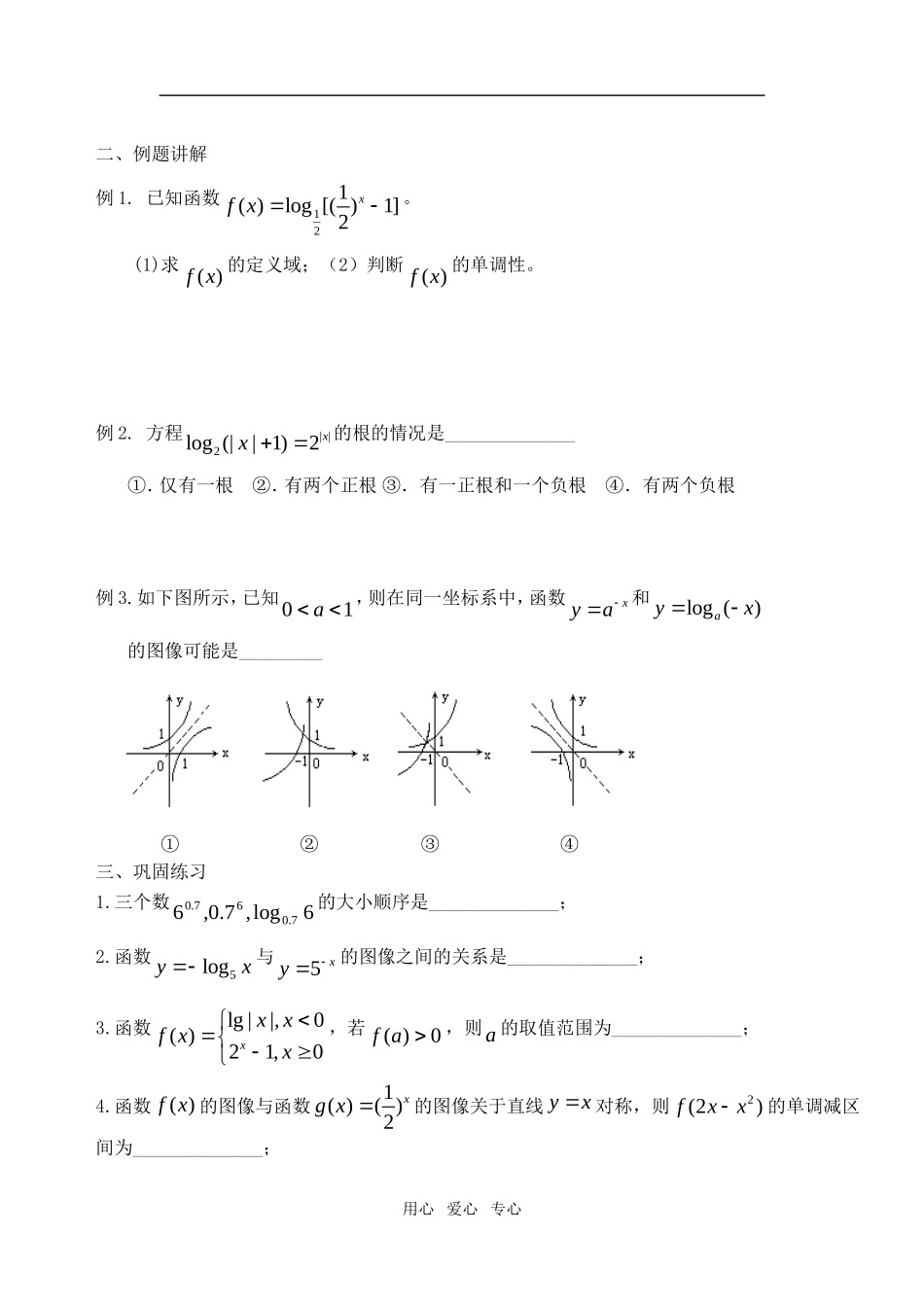
指数函数与对数函数复习一、知识回顾1.staa__________；()sta__________；()tab__________；（其中,,0,0stQab）2.对数(0,1)aa（1）baNb________（2）log1a____；logaa_____；logaNa____0N；logbaa_________（3）logaMN_________；logaMN_________；lognab=_________,0MN（4）换底公式：______________;logmnab＝________；abbaloglog＝_________3.指数函数xya与对数函数logayx(0,1)aa的图象与性质名称指数函数对数函数解析式定义域值域过定点图象当a＞1时，当a＞1时，当0＜a＜1时当0＜a＜1时，单调性当a＞1时当a＞1时当0＜a＜1时当0＜a＜1时图象关系4.函数xya与1()xya图像关于_________对称；函数xya与logayx图像关于_________对称；函数logayx与1logayx图像关于_________对称；用心爱心专心二、例题讲解例1.已知函数121()log[()1]2xfx。(1)求()fx的定义域；（2）判断()fx的单调性。例2.方程||2log(||1)2xx的根的情况是______________①．仅有一根②．有两个正根③．有一正根和一个负根④．有两个负根例3.如下图所示，已知01a，则在同一坐标系中，函数xya和log()ayx的图像可能是_________①②③④三、巩固练习1.三个数6log,7.0,67.067.0的大小顺序是______________；2.函数5logyx与5xy的图像之间的关系是______________；3.函数lg||,0()21,0xxxfxx，若()0fa，则a的取值范围为______________；4.函数()fx的图像与函数1()()2xgx的图像关于直线yx对称，则2(2)fxx的单调减区间为______________；用心爱心专心指数函数与对数函数复习命题：成云荣审核：赵凌昆班级___________姓名___________1.已知)2(logxya是x的增函数，则a的取值范围______________；2.函数)(xf的定义域是（0，1]，则函数(2)xf的定义域____________；3.函数)(xf的定义域是[-1，1]，则函数)(log21xf的定义域____________；4.已知)(xf是对数函数，(61)(61)1ff,则(261)(261)ff=____________；5.已知()log|1|(01)agxxaa且在(1,0)上有()0gx，则|1|()xfxa的单调增区间是____________；6.若函数xay)(log21在R上为增函数，则a的取值范围是____________；7.已知函数f（x）=lg（2x－b）（b为常数），若x∈［1，+∞）时，f（x）≥0恒成立，则b的取值范围是____________；8.已知函数)0(log)0(3)(2xxxxfx，那么)]41([ff的值为____________；9.讨论函数的单调性（1）22log(56)yxx；（2）2561()3xxy；10.讨论下列函数的奇偶性（1）22log(1)1yx；（2）3333xxxxy；用心爱心专心11.设,3log2x求xxxx222233的值。12.已知关于x的方程35432xaa有负根（1）求实数a的值的集合M；（2）若函数()64xfx的定义域恰为M，求()fx的值域；用心爱心专心