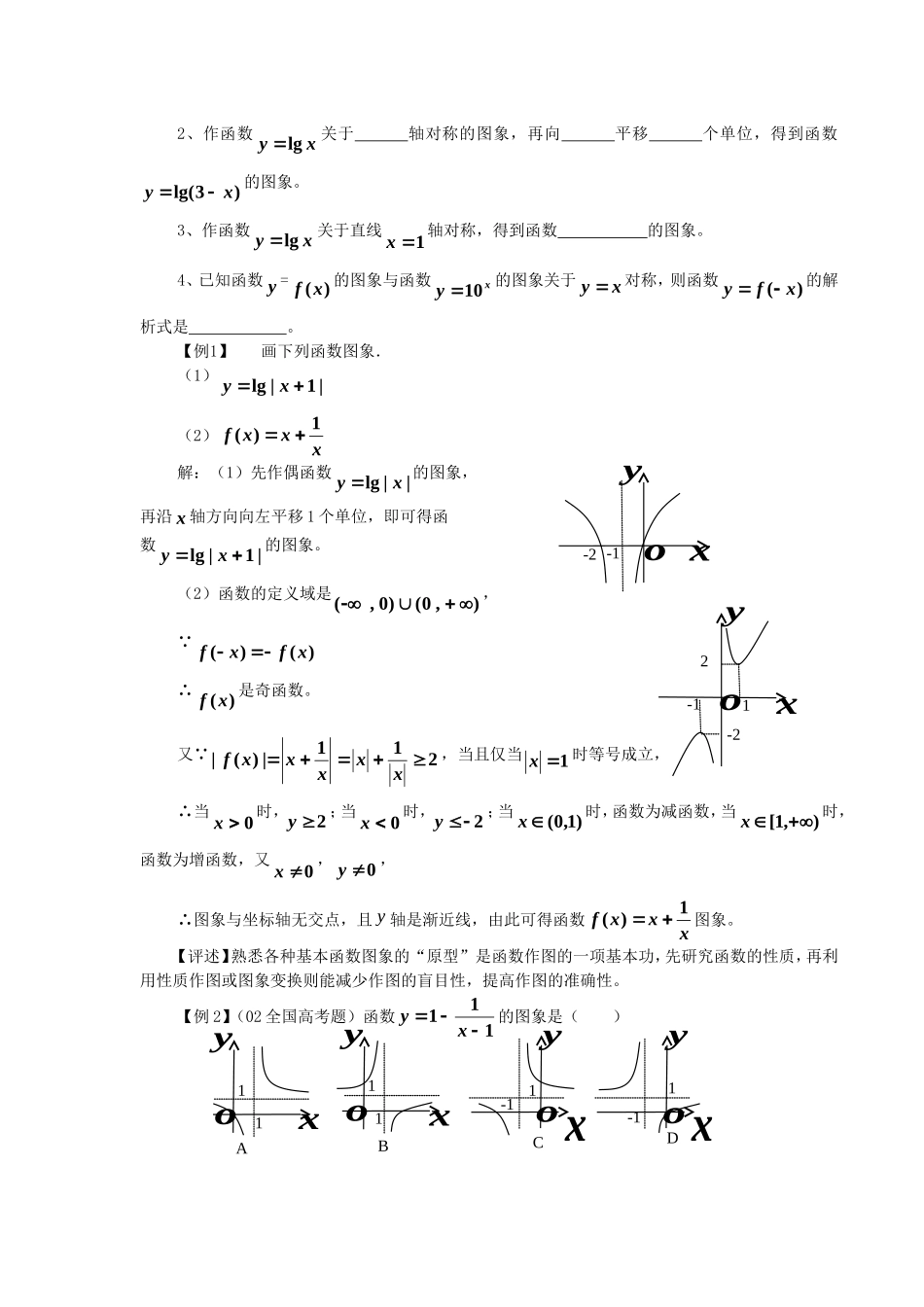
函数的图象一.教学目标:1.熟练掌握基本函数的图象;2.能正确地从函数的图象特征去讨论函数的主要性质;3.能够正确运用数形结合的思想方法解题.二.教学重点:熟练基本函数的图象并掌握图象的初等变换.三.教学过程:(一)主要知识:1.作图方法:描点法和利用基本函数图象变换作图;2.三种图象变换:平移变换、对称变换和伸缩变换等等;3.识图:分布范围、变化趋势、对称性、周期性等等方面.(二)主要方法:1.点的对称点P(x,y)2.平移变换:(1)水平平移:函数()yfxa的图像可以把函数()yfx的图像沿x轴方向向左(0)a或向右(0)a平移||a个单位即可得到;(2)竖直平移:函数()yfxa的图像可以把函数()yfx的图像沿x轴方向向上(0)a或向下(0)a平移||a个单位即可得到.3.对称变换:(1)函数()yfx的图像可以将函数()yfx的图像关于y轴对称即可得到;(2)函数()yfx的图像可以将函数()yfx的图像关于x轴对称即可得到;(3)函数()yfx的图像可以将函数()yfx的图像关于原点对称即可得到;(4)函数1()yfx的图像可以将函数()yfx的图像关于直线yx对称得到.(5)y=-f-1(-x)与y=f(x)的图像关于直线y=-x对称。4.翻折变换:(1)函数|()|yfx的图像可以将函数()yfx的图像的x轴下方部分沿x轴翻折到x轴上方,去掉原x轴下方部分,并保留()yfx的x轴上方部分即可得到;(2)函数(||)yfx的图像可以将函数()yfx的图像右边沿y轴翻折到y轴左边替代原y轴左边部分并保留()yfx在y轴右边部分即可得到.5.伸缩变换:(1)函数()yafx(0)a的图像可以将函数()yfx的图像中的每一点横坐标不变纵坐标伸长(1)a或压缩(01a)为原来的a倍得到;(2)函数()yfax(0)a的图像可以将函数()yfx的图像中的每一点纵坐标不变横坐标伸长(1)a或压缩(01a)为原来的1a倍得到.6.函数图象的对称性:对于函数)(xfy,若对定义域内的任意x都有:①)()(xafxaf(或))2()(xafxf,则)(xf的图象关于直线ax对称;②bxafxaf2)()((或)2)2()(bxafxf,,则)(xf的图象关于点),(baP对称。(三)学习要点:熟练掌握函数图象的有关知识是学习函数以及解决函数问题的重要基本技能,在学习时要抓住下面几个要点:1.学习函数图象的最基本的能力是熟练掌握所学过的基本初等函数(如正、反比例函数,二次函数,指数、对数函数,三角函数)的图象,这些内容将在后面的几讲中作详细的讨论.2.函数图象的变换是学习中的重要内容,大量与函数图象有关的问题都要运用函数图变换的知识.3.函数图象的对称性质是某些函数具有的一种图象性质,在学习中有一定的应用.4.学习函数的基本功是作函数的图象,但在中学数学的学习中,这种能力要求不很高,只须要能作出一些简单的函数的图象,作函数图象的基本步骤是:①讨论函数的定义域及函数的基本性质;②如果函数的图象与图象的变换有关,应考虑运用图象变换作出图象;③作函数的图象必须准确描出关键的点线(如图象与x、y轴的交点,极值点(顶点),对称轴,渐近线,等等);④“数形结合”是一种很重要的数学方法,在解决许多函数、方程、不等式及其它与函数有关的问题时,常常运用“数形结合”的方法解答问题或帮助分析问题,运用“数形结合”解答问题需要有下述能力与经验:1)必须有能力准确把握问题呈现的全部图象特征;2)必须能够列出等价的数学式子表达问题的图象特征。【基础练习】1、把函数xylg图象上所有点的横坐标都缩短到原来的21,纵坐标保持不变,得到函数的图象。2、作函数xylg关于轴对称的图象,再向平移个单位,得到函数)3lg(xy的图象。3、作函数xylg关于直线1x轴对称,得到函数的图象。4、已知函数y=)(xf的图象与函数xy10的图象关于xy对称,则函数)(xfy的解析式是。【例1】画下列函数图象.(1)|1|lgxy(2)xxxf1)(解:(1)先作偶函数||lgxy的图象,再沿x轴方向向左平移1个单位,即可得函数|1|lgxy的图象。(2)函数的定义域是),0()0,(, )()(xfxf∴)(xf是奇函数。又 211|)(|xxxxxf,当且仅当1x...