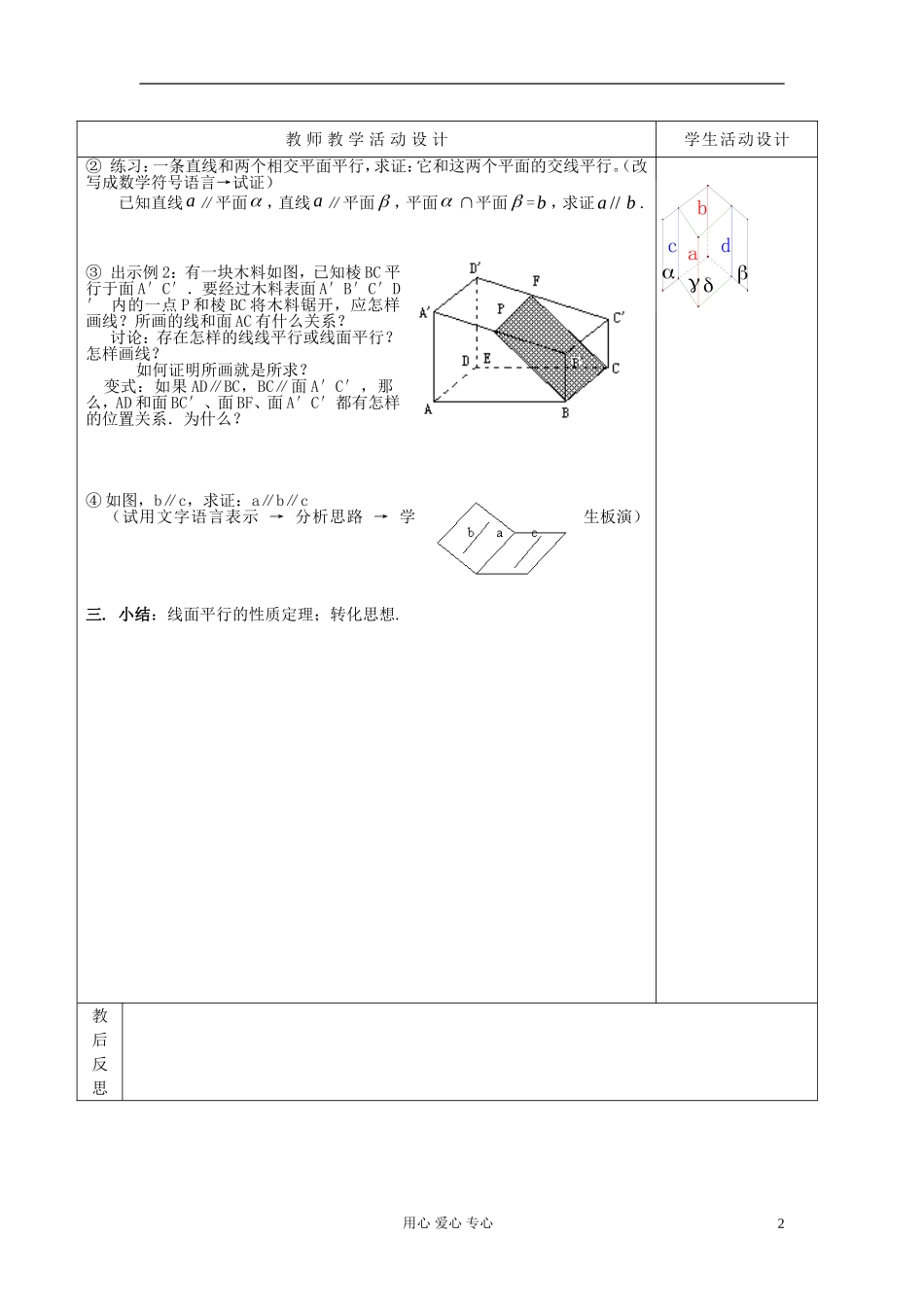
课题2.2.3直线与平面平行的性质课时第课时课型新授课授课班级课时教学目标掌握直线和平面平行的性质定理,灵活运用线面平行的判定定理和性质定理,掌握“线线”“线面”平行的转化.教学重点、难点重点:掌握线面平行的性质定理.难点:掌握“线线”“线面”平行之间的转化教学方法实验用具及教具教学过程设计教师教学活动设计学生活动设计一、复习准备:1.提问:线面平行、面面平行判定定理?符号语言?图形语言?2.讨论:①直线与一个平面平行,那么这条直线和平面内的直线有何位置关系?②直线a与一个平面平行,在平面内如何作一条直线与直线a平行?二、讲授新课:1.教学线面平行的性质定理:①讨论:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线的位置关系如何?②给出线面性质定理及符号语言://,,//llmlm.③讨论性质定理的证明:∵//l,∴l和没有公共点,又∵m,∴l和m没有公共点;即l和m都在内,且没有公共点,∴//lm.④讨论:如果过平面内一点的直线平行于与此平面平行的一条直线,那么这条直线是否在此平面内?如果两条平行直线中的一条平行于一个平面,那么另一条与平面有何位置关系?2.教学例题:①出示例1:已知直线a∥直线b,直线a∥平面α,bα,求证:b∥平面α分析:如何作辅助平面?→怎样进行平行的转化?→师生共练→小结:作辅助平面;转化思想“线面平行→线线平行→线线平行→线面平行教学过程设计用心爱心专心1mlcaαcaαβb教师教学活动设计学生活动设计②练习:一条直线和两个相交平面平行,求证:它和这两个平面的交线平行。(改写成数学符号语言→试证)已知直线a∥平面,直线a∥平面,平面平面=b,求证//ab.③出示例2:有一块木料如图,已知棱BC平行于面A′C′.要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开,应怎样画线?所画的线和面AC有什么关系?讨论:存在怎样的线线平行或线面平行?怎样画线?如何证明所画就是所求?变式:如果AD∥BC,BC∥面A′C′,那么,AD和面BC′、面BF、面A′C′都有怎样的位置关系.为什么?④如图,b∥c,求证:a∥b∥c(试用文字语言表示→分析思路→学生板演)三.小结:线面平行的性质定理;转化思想.教后反思用心爱心专心2dcba