测量误差的合成和分配VIP免费

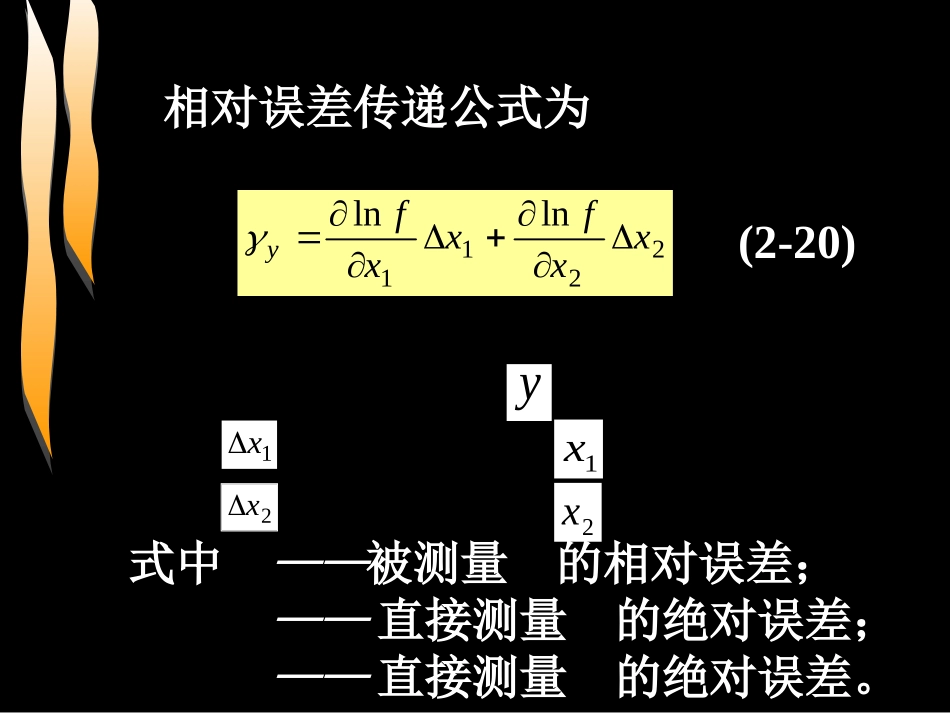
2.4测量误差的合成和分配误差合成理论研究在间接测量中，如何根据若干个直接测量量的误差求总测量误差的问题；误差分配理论则研究在给定系统总误差的条件下，如何将总误差分配给各测量分项，即如何对各分项误差提出要求，以达到系统测量精度要求。1．误差传递公式设一个被测量由两个分项、，其函数表达式为则绝对误差传递公式为式中——被测量的绝对误差；——直接测量量的绝对误差；——直接测量量的绝对误差。y1x2x21,xxfy2211xxfxxfyyy1x2x1x2x2.4.1测量误差的合成(2-18)(2-19)相对误差传递公式为式中——被测量的相对误差；——直接测量的绝对误差；——直接测量的绝对误差。2211lnlnxxfxxfyy1x2xy1x2x(2-20)同理，当被测量由m个分项合成时,误差传递公式为式中——第i个测量分项的测量值；——直接测量量的绝对误差。一般，若的函数关系为和、差关系时，常先求总合的绝对误差，若函数关系为积、商或乘方、开方关系时，常先求总合的相对误差比较方便。imiixxfy1miiiyxxf1lnixixmxxxfy,,21ixy(2-21)(2-22)•例1：用间接测量法测量电阻消耗的功率，若电阻、电压和电流测量相对误差分别为、和，问所求功率的相对误差为多少？•例2：用伏安法测电阻时，若测量电压和电流的相对误差为、，试问所求电阻的相对误差为多少？若为±4%，为±3%，为多少？UUIIRRuiuiR2．系统误差的合成若测量中各种随机误差可以忽略，则总和的系统误差可由各分项系统误差合成。式中——系统误差的总和；——直接测量各分项的系统误差。jmjjyxf1yj(2-23)3．随机误差的合成若各分项的系统误差为零，则同理可求总合的随机误差式中——随机误差的总和；——直接测量各分项的随机误差。jmjjyxfˆˆ1yˆjˆ(2-24)已知各分项方差，求总合方差的公式为标准差的计算公式为jmjjxxfx1222ˆˆjmjjxxfxˆˆ12(2-25)(2-26)1．等准确度分配当总误差中各分项性质相同（量纲相同）、大小相近时，采用等准确度分法，即分配给各分项的误差彼此相同。若总误差为，各分项的误差为；标准差为，令；，则分配给各项的误差为ym，，21mxxxˆˆˆ21、、、m21ˆˆˆˆ21mxxxmjxfmjjyj3211，，mjjjxfyx12ˆˆ2.4.2测量误差的分配(2-27)(2-28)•例：有一个电源变压器，已知初级线圈与两个次级线圈的匝数比N12:N34:N45=1:2:2，用最大量程为500V的交流电压表测量次级线圈的总电压，要求相对误差小于±2%，问应该选用哪个级别的电压表？2．等作用分配当分项误差性质不同时，采用等作用分配方法。在这种分配方式中，分配给各分项的误差在数值上不一定相等，但它们对测量误差总和的作用是相同的。对于系统误差，在式（2-23）中，令。则分配给各分项的误差为mmfxfxf2211jyjxfm(2-29)对于随机误差，在式（2-25）中，令，则分配给各分项的误差为mmxxfxxfxxf2222221221ˆˆˆjjxfmyxˆˆ(2-30)•例：间接测量电阻上消耗的功率，已测出电流为100mA，电压为3V，算出功率为300mW，若要求功率测量的系统误差不大于5%，随机误差的标准差不大于5mW，问电压和电流的测量误差应在多大范围内，才能保证上述功率误差的要求。3．抓住主要误差项进行分配当分项误差中某项误差特别大时，就可以不考虑次要分项的误差，或酌情分给次要分项少量误差比例，确保主要项的误差小于总合的误差。若主要误差项有若干项，这时可把误差在这几个主要误差项中分配，考虑采用等准确度或等作用分配原则。2.5测量结果的描述与处理对测量结果可采用正确度，精密度和准确度三种评价方法。1．正确度表示测量结果中系统误差大小程度。系统误...