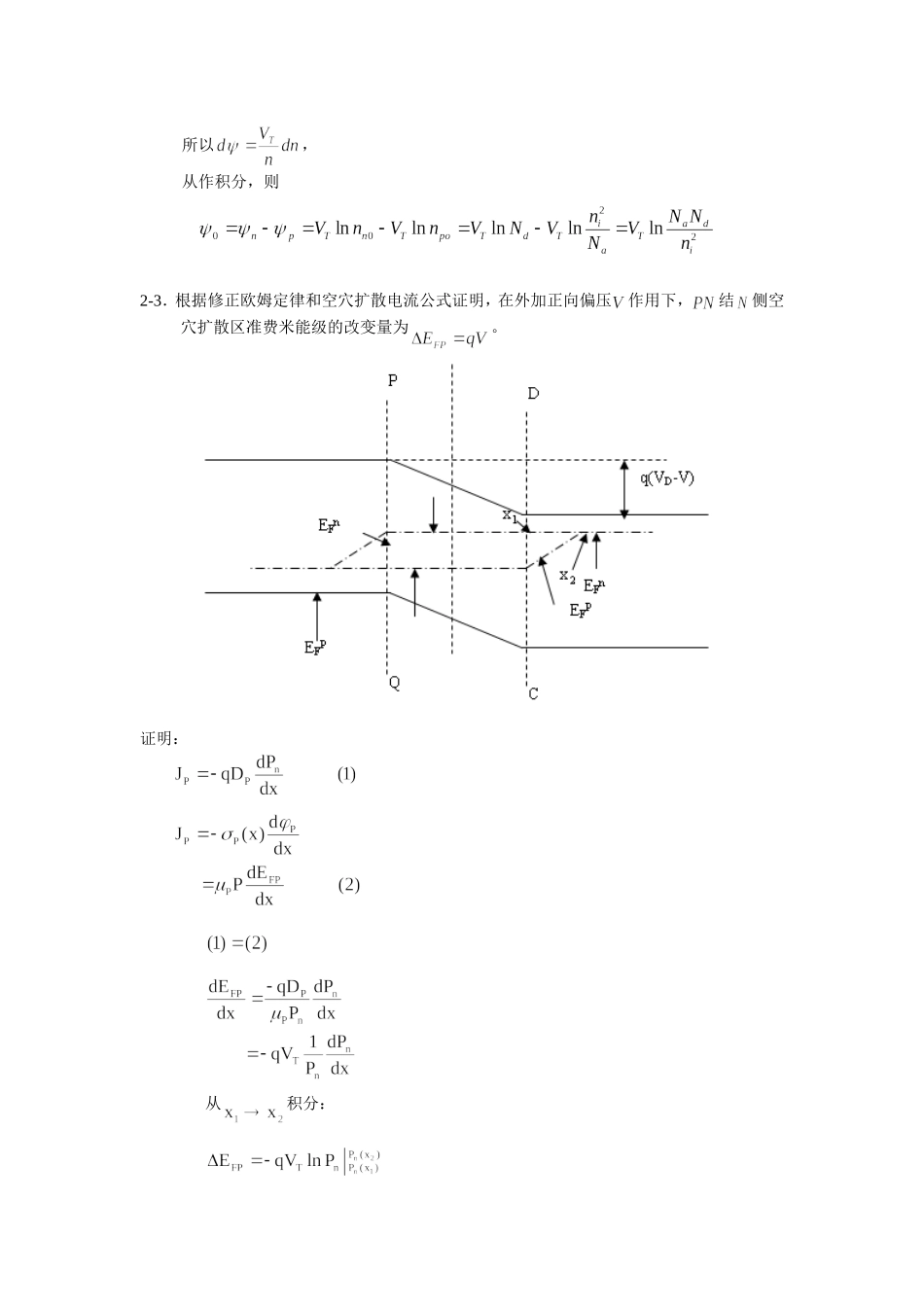
2-1.结空间电荷区边界分别为和,利用导出表达式。给出N区空穴为小注入和大注入两种情况下的表达式。解:在处而()(此为一般结果)小注入:()大注入:且所以或2-2.热平衡时净电子电流或净空穴电流为零,用此方法推导方程。解:净电子电流为处于热平衡时,In=0,又因为所以,又因为(爱因斯坦关系)所以,从作积分,则2-3.根据修正欧姆定律和空穴扩散电流公式证明,在外加正向偏压作用下,结侧空穴扩散区准费米能级的改变量为。证明:从积分:将代入得2-4.硅突变结二极管的掺杂浓度为:,,在室温下计算:(a)自建电势(b)耗尽层宽度(c)零偏压下的最大内建电场。解:(a)自建电势为(b)耗尽层宽度为(с)零偏压下最大内建电场为2–5.若突变结两边的掺杂浓度为同一数量级,则自建电势和耗尽层宽度可用下式表示试推导这些表示式。解:由泊松方程得:积分一次得由边界条件所以再积分一次得令得:,于是再由电势的连续性,当x=0时,:所以再由得故将代入上式,得2–6.推导出线性缓变结的下列表示式:(a)电场(b)电势分布(c)耗尽层宽度(d)自建电势。解:在线性缓变结中,耗尽层内空间电荷分布可表示为Nd-Na=axa为杂质浓度斜率设由泊松方程得积分为当时=0,即所以且对式再积分一次得因为当时,当时,故2-7.推导出结(常称为高低结)内建电势表达式。解:结中两边掺杂浓度不同(),于是区中电子向区扩散,在结附近区形成,区出现多余的电子。二种电荷构成空间电荷,热平衡时:令则即空间电荷区两侧电势差。2-8.(a)绘出图2-6a中的扩散结的杂质分布和耗尽层的草图。解释为何耗尽层的宽度和的关系曲线与单边突变结的情况相符。(b)对于的情况,重复(a)并证明这样的结在小的行为像线性结,在大时像突变结。2-9.对于图2-6(b)的情况,重复习题2-8。2–10.(a)结的空穴注射效率定义为在处的,证明此效率可写成(b)在实际的二极管中怎样才能使接近1。证明(a):而,所以(b)则因为,而,,所以即所以,即,即受主杂质浓度远大与施主杂质浓度。2-11.长结二极管处于反偏压状态,求:(1)解扩散方程求少子分布和,并画出它们的分布示意图。(2)计算扩散区内少子贮存电荷。(3)证明反向电流为结扩散区内的载流子产生电流。解:(1)其解为(1)边界条件:有将代入(1):(2)此即少子空穴分布。类似地求得(2)少子贮存电荷这是N区少子空穴扩散区内的贮存电荷,说明贮存电荷是负的,这是反向PN结少子抽取的现象。同理可求得。说明贮存电荷是正的(电子被抽取,出现正的电离施主)。(3)假设贮存电荷均匀分布在长为的扩散区内,则X0nxXXXXX在空穴扩散区,复合率在电子扩散区,复合率,可见,则空穴扩散区内少子产生率为,电子扩散区内少子产生率为。与反向电流对比:可见,PN结反向电流来源于扩散区内产生的非平衡载流子。2-12.若结边界条件为处,处。其中和分别与与具有相同的数量级,求、以及、的表达式。解:(2),(3)分别代入(1)得:从中解出:(4)(5)将(4)(5)代入(1):(6)(6)式即为N侧空穴分布。类似的,讨论:(1)即长PN结:,分子分母第二项近似为0(此即长PN结中少子分布)即短PN结:若取(坐标原点),则对的讨论类似有(取)对于短二极管:(取)(取)2–13.在结二极管中,N区的宽度远小于Lp,用(S为表面复合速度)作为N侧末端的少数载流子电流,并以此为边界条件之一,推导出载流子和电流分布。絵出在S=0和S=时N侧少数载流子的分布形状。解:连续方程,由边界条件,得,由上述条件可得所以讨论S=0:x=0,X=2-14.推导公式(2-72)和(2-73)。2–15.把一个硅二极管用做变容二极管。在结的两边掺杂浓度分别为以及。二极管的面积为100平方密尔。(a)求在和时的二极管的电容。(b)计算用此变容二极管及的储能电路的共振频率。(注:(密耳)为长度单位,(英寸))解:(a)因为所以(1平方密尔=)VR=1V当VR=5V时(b)当谐振频率和控制电压有线性关系时:当VR=1V,当VR=5V,2-16.用二极管恢复法测量二极管空穴寿命。(a)对于和,在具有上升时间的示波器上测得,求。(b)若(a)中快速示波器无法得到,只得采用一只具有上升时间较慢的示...