高等数学习题答案 人民大学出版社 第6章 应用1VIP免费

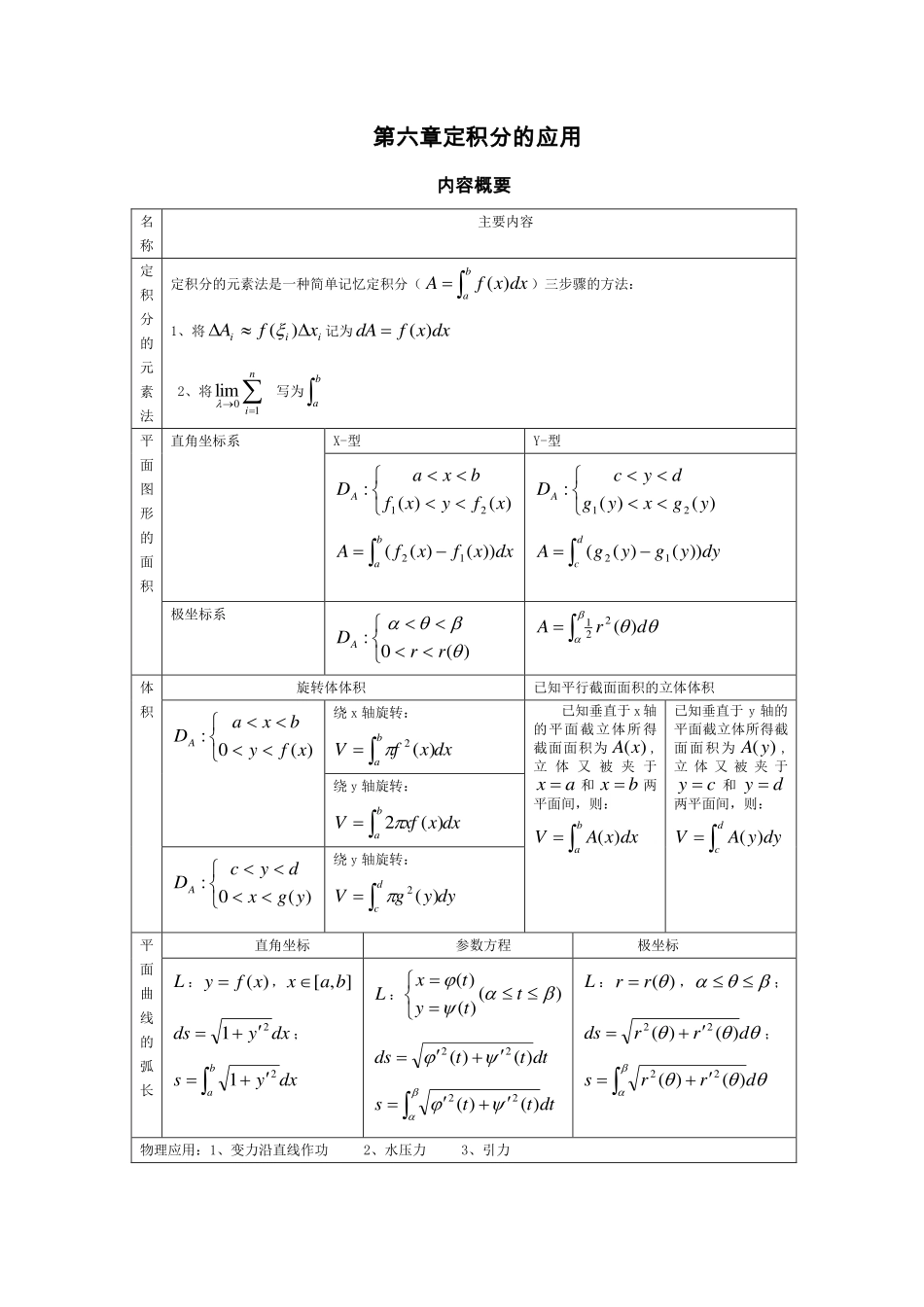
第六章定积分的应用内容概要名称主要内容定积分的元素法定积分的元素法是一种简单记忆定积分（badxxfA)(）三步骤的方法：1、将iiixfA)(记为dxxfdA)(2、将ni10lim写为ba平面图形的面积直角坐标系X-型Y-型)()(:21xfyxfbxaDAbadxxfxfA))()((12)()(:21ygxygdycDAdcdyygygA))()((12极坐标系)(0:rrDAdrA)(221体积旋转体体积已知平行截面面积的立体体积)(0:xfybxaDA绕x轴旋转：dxxfVba)(2已知垂直于x轴的平面截立体所得截面面积为)(xA,立体又被夹于ax和bx两平面间，则：badxxAV)(已知垂直于y轴的平面截立体所得截面面积为)(yA,立体又被夹于cy和dy两平面间，则：dcdyyAV)(绕y轴旋转：dxxxfVba)(2)(0:ygxdycDA绕y轴旋转：dyygVdc)(2平面曲线的弧长直角坐标参数方程极坐标L：)(xfy，],[baxdxyds21；badxys21L：)()()(ttytxdtttds)()(22dttts)()(22L：)(rr，；drrds)()(22；drrs)()(22物理应用：1、变力沿直线作功2、水压力3、引力x0y1图6-2-1yxyxDx0y/2/2图6-2-2sinyx1D课后习题全解习题6-2★1．求由曲线xy与直线xy所围图形的面积。知识点：平面图形的面积思路：由于所围图形无论表达为X-型还是Y-型，解法都较简单，所以选其一做即可解：见图6-2-1 所围区域D表达为X-型：xyxx10，（或D表达为Y-型：yxyy210）∴10)(dxxxSD61)2132(10223xx（10261)(dyyySD）★2．求在区间[0，/2]上，曲线xysin与直线0x、1y所围图形的面积知识点：平面图形面积思路：由于所围图形无论表达为X-型还是Y-型，解法都较简单，所以选其一做即可解：见图6-2-2x0y4图6-2-32yx22224yxD 所围区域D表达为X-型：1sin20yxx，（或D表达为Y-型：yxyarcsin010）∴12)cos()sin1(2020xxdxxSD（12arcsin10ydySD）★★3．求由曲线xy2与42xy所围图形的面积知识点：平面图形面积思路：由于所围图形表达为Y-型时解法较简单，所以用Y-型做解：见图6-2-3 两条曲线的交点：22422yxxyxy，∴所围区域D表达为Y-型：22422yxyy，∴2316)324()4(2232222yydyyySD（由于图形关于X轴对称，所以也可以解为：2316)324(2)4(22032022yydyyySD）★★4．求由曲线2xy、24xy、及直线1y所围图形的面积知识点：平面图形面积思路：所围图形关于Y轴对称，而且在第一象限内的图形表达为Y-型时，解法较简单解：见图6-2-4 第一象限所围区域1D表达为Y-型：yxyy210，∴34322)2(221023101ydyyySSDD（若用X-型做，则第一象限内所围区域1DbaDD，其中aD：22410xyxx，bD：14212yxx；∴12212201422[()(1)]443DDxxSSxdxdx）★★5．求由曲线xy1与直线xy及2x所围图形的面积知识点：平面图形面积思路：由于所围图形表达为X-型,解法较简单，所以用X-型做x0y1图6-2-4224yxyx12D1Dx0y1图6-2-5yx1/yx21Dx0y图6-2-622yx021D解：见图6-2-5 两条曲线xy1和xy的交点为（1，1）、（-1，-1），又这两条线和2x分别交于)21,2(、2),2(∴所围区域D表达为X-型：xyxx121，∴22211113()(ln)ln222DSxdxxxx★★★6．抛物线xy22分圆822yx的面积为两部分，求这两部分的面积知识点：平面图形面积思路：所围图形关于X轴对称，而且在第一象限内的图形表达为Y-型时，解法较简单解：见图6-2-6，设阴影部分的面积为1DS，剩余面积为2DS 两条曲线xy22、822yx的交于(2,2)（舍去4x的解），∴所围区域1D表达为Y-型：228222yxyy；又图形关于x轴对称，∴342)342(2)68(2...