离散数学习题六答案刘爱民 VIP免费

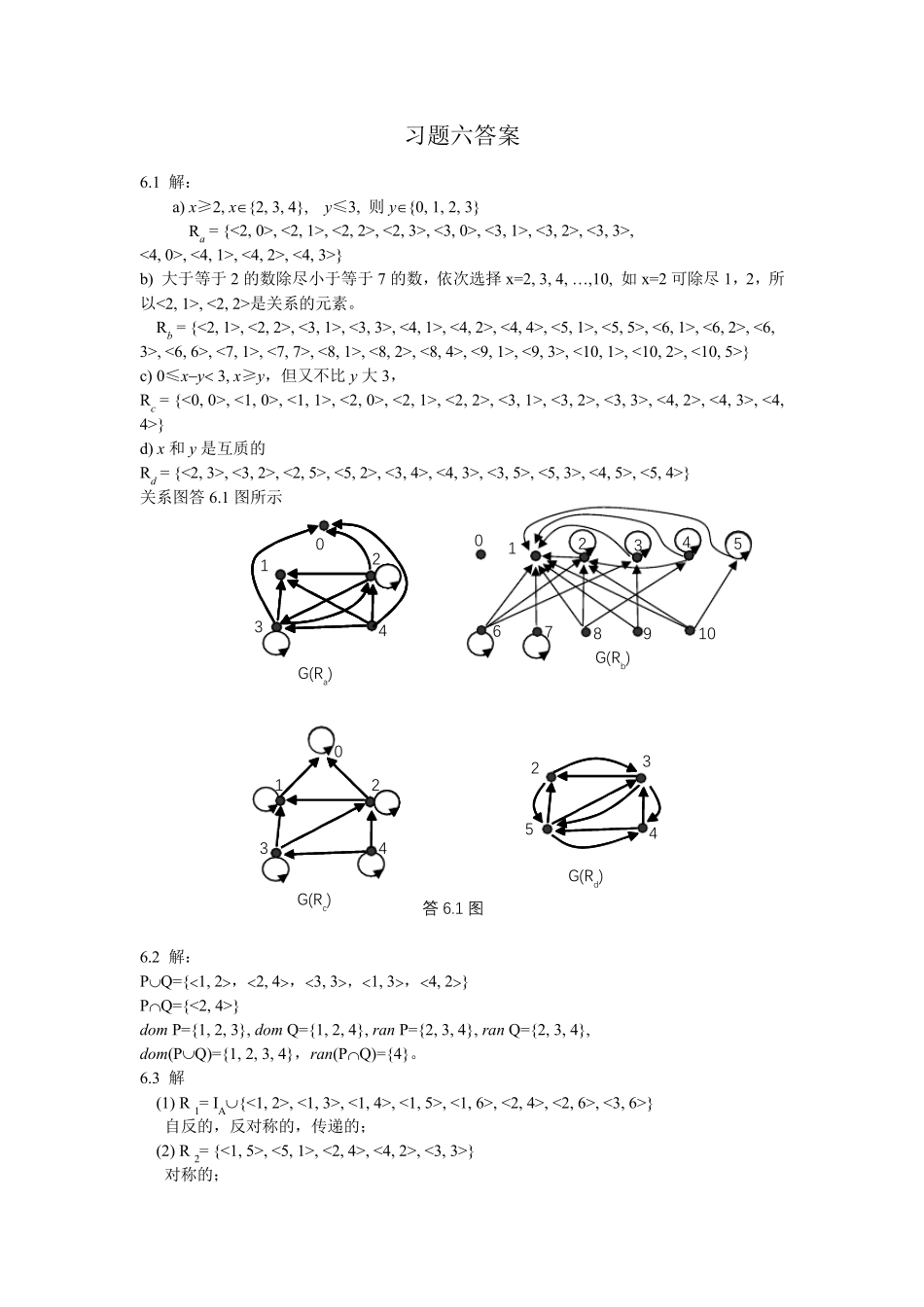
习题六答案6.1解：a)x≥2,x{2,3,4},y≤3,则y{0,1,2,3}Ra={<2,0>,<2,1>,<2,2>,<2,3>,<3,0>,<3,1>,<3,2>,<3,3>,<4,0>,<4,1>,<4,2>,<4,3>}b)大于等于2的数除尽小于等于7的数，依次选择x=2,3,4,…,10,如x=2可除尽1，2，所以<2,1>,<2,2>是关系的元素。Rb={<2,1>,<2,2>,<3,1>,<3,3>,<4,1>,<4,2>,<4,4>,<5,1>,<5,5>,<6,1>,<6,2>,<6,3>,<6,6>,<7,1>,<7,7>,<8,1>,<8,2>,<8,4>,<9,1>,<9,3>,<10,1>,<10,2>,<10,5>}c)0≤xy3,x≥y，但又不比y大3，Rc={<0,0>,<1,0>,<1,1>,<2,0>,<2,1>,<2,2>,<3,1>,<3,2>,<3,3>,<4,2>,<4,3>,<4,4>}d)x和y是互质的Rd={<2,3>,<3,2>,<2,5>,<5,2>,<3,4>,<4,3>,<3,5>,<5,3>,<4,5>,<5,4>}关系图答6.1图所示6.2解：PQ={1,2，2,4，3,3，1,3，4,2}PQ={<2,4>}domP={1,2,3},domQ={1,2,4},ranP={2,3,4},ranQ={2,3,4},dom(PQ)={1,2,3,4}，ran(PQ)={4}。6.3解(1)R1=IA{<1,2>,<1,3>,<1,4>,<1,5>,<1,6>,<2,4>,<2,6>,<3,6>}自反的，反对称的，传递的；(2)R2={<1,5>,<5,1>,<2,4>,<4,2>,<3,3>}对称的；1234G(Ra)01234G(Rc)02354G(Rd)答6.1图G(Rb)123405678910