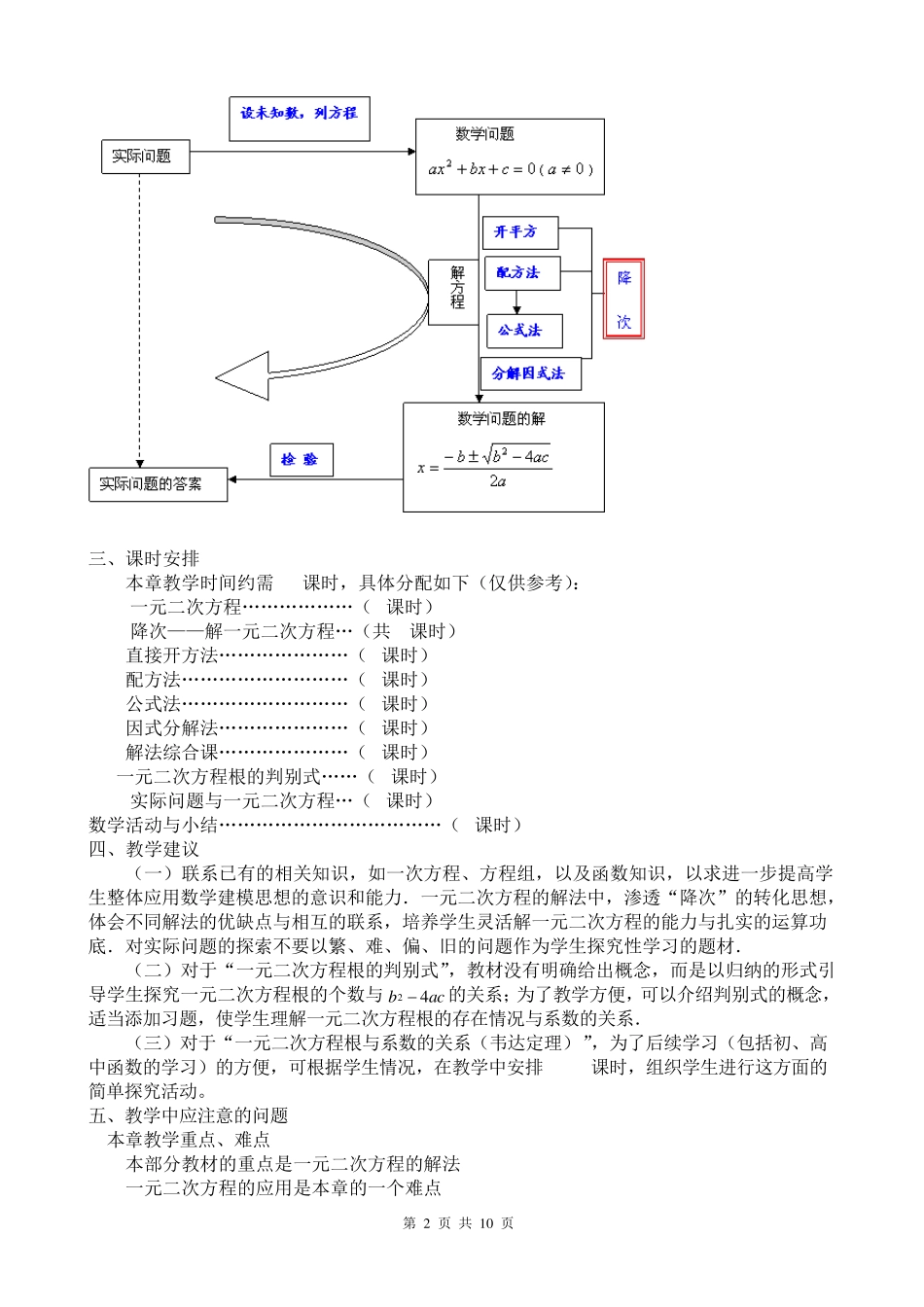
第1页共10页第二十一章一元二次方程教材分析及相关练习一、(一)课程学习目标课标要求理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程;会用一元二次方程根的判别式判别方程是否有实根和两个实根是否相等;*了解一元二次方程的根与系数的关系。1.联系一元一次方程和函数的基本知识,继续探索实际问题中的数量关系及其变化规律,让学生进一步体会“方程是刻画现实世界的一个有效的数学模型”.2.以分析实际问题中的等量关系并求解其中的未知数为背景,认识一元二次方程及其有关概念.3.根据化归的思想,抓住“降次”这一基本策略,掌握开平方法、配方法、公式法和因式分解法等一元二次方程的基本解法.4.经历分析和解决实际问题的过程,体会一元二次方程的数学模型作用,进一步提高在实际问题中运用方程这种重要数学工具的基本能力.(二)中考考试要求:源自《2017中考说明》ABC一元二次方程了解一元二次方程的有关概念;理解配方法;会用一元二次方程的根的判别式判断方程根的情况能用适当的方法解数字系数的一元二次;能用根的判别式解决与一元二次方程根有关的问题运用方程与不等式的有关内容解决有关问题(2016)考试内容考试要求ABC一元二次方程了解一元二次方程的有关概念.理解配方法;会用一元二次方程根的判别式判断方程根的情况.能选择适当的方法解数字系数一元二次方程;能有根的判别式解决与一元二次方程根有关的问题运用方程有关内容解决有关问题二、本章知识结构框图第2页共10页三、课时安排本章教学时间约需16课时,具体分配如下(仅供参考):22.1一元二次方程………………(1课时)22.2降次——解一元二次方程…(共9课时)直接开方法…………………(1课时)配方法………………………(1课时)公式法………………………(2课时)因式分解法…………………(2课时)解法综合课…………………(1课时)一元二次方程根的判别式……(2课时)22.3实际问题与一元二次方程…(4课时)数学活动与小结………………………………(2课时)四、教学建议(一)联系已有的相关知识,如一次方程、方程组,以及函数知识,以求进一步提高学生整体应用数学建模思想的意识和能力.一元二次方程的解法中,渗透“降次”的转化思想,体会不同解法的优缺点与相互的联系,培养学生灵活解一元二次方程的能力与扎实的运算功底.对实际问题的探索不要以繁、难、偏、旧的问题作为学生探究性学习的题材.(二)对于“一元二次方程根的判别式”,教材没有明确给出概念,而是以归纳的形式引导学生探究一元二次方程根的个数与24bac的关系;为了教学方便,可以介绍判别式的概念,适当添加习题,使学生理解一元二次方程根的存在情况与系数的关系.(三)对于“一元二次方程根与系数的关系(韦达定理)”,为了后续学习(包括初、高中函数的学习)的方便,可根据学生情况,在教学中安排1~2课时,组织学生进行这方面的简单探究活动。五、教学中应注意的问题本章教学重点、难点1.本部分教材的重点是一元二次方程的解法2.一元二次方程的应用是本章的一个难点第3页共10页3.培养学生注意观察一元二次方程的结构特征,正确地选用适当方法解一元二次方程是本章的一个重点,也是一个难点.(一)、一元二次方程的概念1.理解并掌握一元二次方程的意义未知数个数为1,未知数的最高次数为2,整式方程,可化为一般形式;2.正确识别一元二次方程中的各项及各项的系数(1)让学生明确只有当二次项系数0a时,整式方程02cbxax才是一元二次方程。(2)各项的确定(包括各项的系数及各项的未知数).(3)让学生熟练整理方程的过程3.一元二次方程的解的定义与检验一元二次方程的解4.列出实际问题的一元二次方程(二)、一元二次方程的解法1.让学生明确一元二次方程是以降次为目的,以配方法、开平方法、公式法、因式分解法等方法为手段,从而把一元二次方程转化为一元一次方程求解;2.要让学生能观察方程系数的特点,熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程;3.引导学生体会不同解法的相互的联系;4.值得注意的几个问题:(1)开平方法:对于形如nx2或)0...