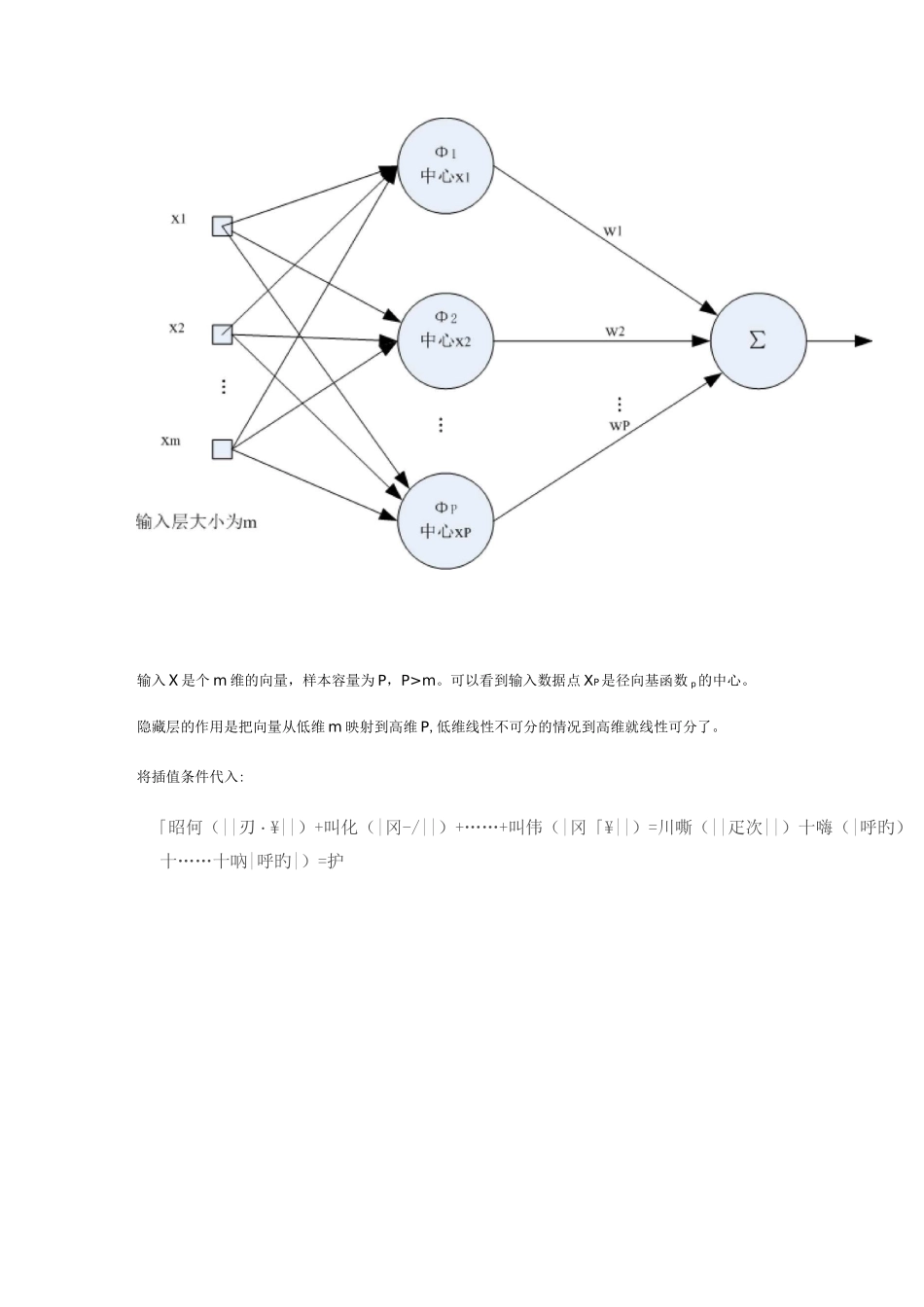
DDDDDDDDDDDDDDCMACDDDDBDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDPDRBFDDDDDDD+叫伟(11DDDDDDDDDRBFDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDBPDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDRBFDDDDDDDDDDDDDDDDDDDPDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD2ODDDDDDDDDDDDDDDDD尸(对=》旳竹(||苗用||)=叭©(||炉屮||)十叫仞(||苗/||)+卩=LDDDDDDRBFDDDDDRBFDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD输入X是个m维的向量,样本容量为P,P>m。可以看到输入数据点XP是径向基函数p的中心。隐藏层的作用是把向量从低维m映射到高维P,低维线性不可分的情况到高维就线性可分了。将插值条件代入:「昭何(||刃・¥||)+叫化(|冈-/||)+……+叫伟(|冈「¥||)=川嘶(||疋次||)十嗨(|呼旳)十……十吶|呼旳|)=护n^-xj||)+iv2^2(n^-r||)+……+%竹(II枣「糾|)二岀写成向量的形式为叫,显然是个规模这P对称矩阵,且与X的维度无关,当可逆时,对于一大类函数,当输入的X各不相同时,就是可逆的。下面的几个函数就属于这一大类函数:1)Gauss(高斯)函数爭(F)=E®()2(7-2)ReflectedSigmoidal(反常S型)函数1卩(F)=;—厂(7_3)Inversemultiquadrics(拟多二次)函数1卩(F)=—”1-Vr+(y-称为径向基函数的扩展常数,它反应了函数图像的宽度,越小,宽度越窄,函数越具有选择性。完全内插存在一些问题:1)插值曲面必须经过所有样本点,当样本中包含噪声时,神经网络将拟合出一个错误的曲面,从而使泛化能力下降。由于输入样本中包含噪声,所以我们可以设计隐藏层大小为K,KVP,从样本中选取K个(假设不包含噪声)作为函数的中心。3DDDDDDDDDDDDDDDDDD隐藏圧大小为2DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDFDDDDDDDDD1.DDDDD2.DDDDD3.DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDF(X)DDDDDDDDDDDDDDDDOG(X,XP)叮GreenODDGDDGreenODDGreenDDDDDDDDDDDDDDDDDDDDDDDDDDDD(八、'■门HIIfGreenDDDDDDDDDDCoverDDDDminF尸i匚DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDF(X)DDDDDDDDDDDDDDDDDDDDDD||DF||DDDDDDDDDDDDDF(x)DDDD(1)DDDDp=lW^(G+UYld^^*******************************(2)DDGaussODD1G(X、Xgq(||X^||-)2cr-ODDRBFDDDDDDDPODDDDDDDDDDDPDDDpDDDDDDDDDDDDG(X,XP)0□□□□DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD1,DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDGreenDDDDD(2)DDDDDDDDRBFDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD广义RBF网络:从输入层到隐藏层相当于是把低维空间的数据映射到高维空间,输入层细胞个数为样本的维度,所以隐藏层细胞个数一定要比输入层细胞个数多。从隐藏层到输出层是对高维空间的数据进行线性分类的过程,可以采用单层感知器常用的那些学习规则,参见神经网络基础和感知器。注意广义RBF网络只要求隐藏层神经元个数大于输入层神经元个数,并没有要求等于输入样本个数,实际上它比样本数目要少得多。因为在标准RBF网络中,当样本数目很大时,就需要很多基函数,权值矩阵就会很大,计算复杂且容易产生病态问题。另外广RBF网与传统RBF网相比,还有以下不同:1-径向基函数的中心不再限制在输入数据点上,而由训练算法确定。2-各径向基函数的扩展常数不再统一,而由训练算法确定。3-输出函数的线性变换中包含阈值参数,用于补偿基函数在样本集上的平均值与目标值之间的差别。因此广义RBF网络的设计包括:结构设计--隐藏层含有几个节点合适参数设计--各基函数的数据中心及扩展常数、输出节点的权值。下面给出计算数据中心的两种方法:1.数据中心从样本中选取。样本密集的地方多采集一些。各基函数采用统一的偏扩展常数:yflMdmax是所选数据中心之间的最大距离,M是数据中心的个数。扩展常数这么计算是为了避免max径向基函数太尖或太平。2-自组织选择法,比如对样本进...